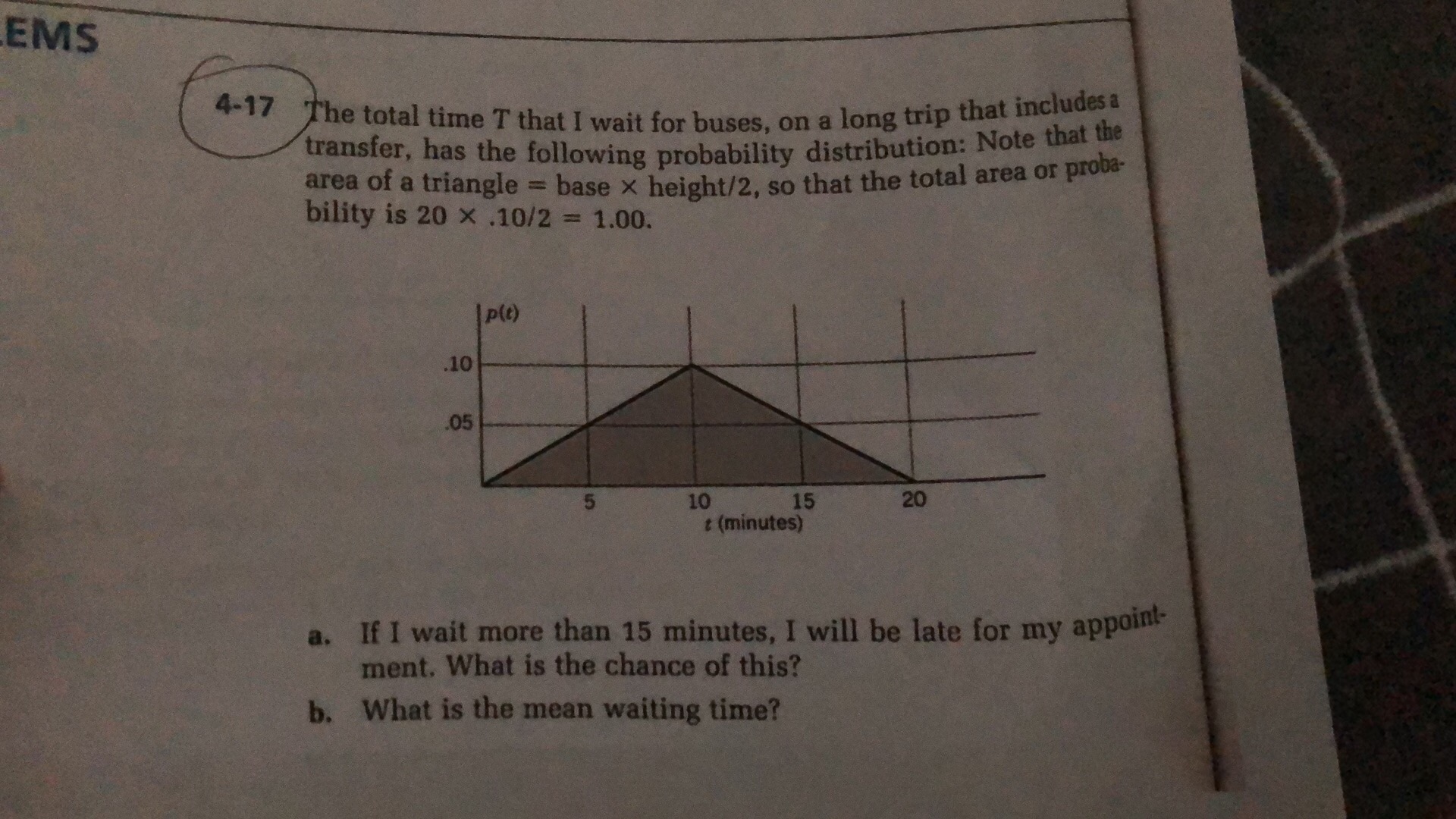
EMS 4 - 17 The total time I that I wait for buses , on a long trip that includes a transfer , has the following probability distribution : Note that the area of a triangle = base x height / 2 , so that the total area or proba- bility is 20 X . 10/2 = 1.00 . | P(! ) . 10 - 05 10 15 20 + ( minutes ) a . If I wait more than 15 minutes , I will be late for my appoint- ment . What is the chance of this ?" b . What is the mean waiting time ?istribution, it helps to know that nearly all of the or probability lies within 3 standard deviations of the mean. (By looking up z = 3 in the standard normal table, we find the probability is 99.7%.) This is shown, along with several other areas, in Figure 4-10. SV Recall that Table IV is repeated inside the front cover where it is easy to find. 4-19 If Z is a standard normal variable, calculate: a. Pr(Z > 1.60) e. Pr(0 20) Y