Given:

	E(R1) = 0.12
	E(R2) = 0.17
	E(1) = 0.04
	E(2) = 0.05

Calculate the expected returns and expected standard deviations of a two-stock portfolio having a correlation coefficient of 0.65 under the conditions given below. Do not round intermediate calculations. Round your answers to four decimal places.

1. w₁ = 1.00

   Expected return of a two-stock portfolio:

   Expected standard deviation of a two-stock portfolio:

2. w₁ = 0.80

   Expected return of a two-stock portfolio:

   Expected standard deviation of a two-stock portfolio:

3. w₁ = 0.55

   Expected return of a two-stock portfolio:

   Expected standard deviation of a two-stock portfolio:

4. w₁ = 0.30

   Expected return of a two-stock portfolio:

   Expected standard deviation of a two-stock portfolio:

5. w₁ = 0.05

   Expected return of a two-stock portfolio:

   Expected standard deviation of a two-stock portfolio:

Choose the correct riskreturn graph for weights from parts (a) through (e) when r_i,j = -0.65; 0.00; 0.65.

The correct graph is -Select-graph Agraph Bgraph Cgraph DItem 11 .

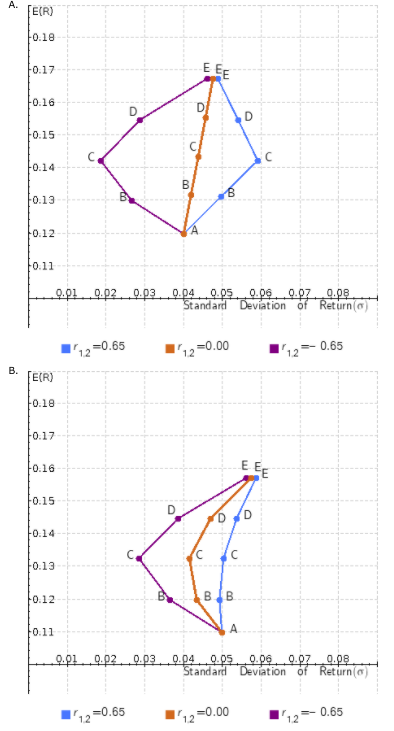
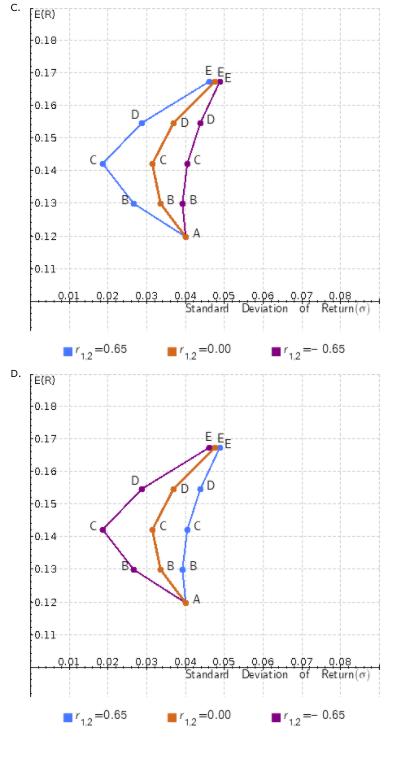
A. FE(R) 0.18 F0.17 EEE 10.16 D 0.15 F0.14 . B F0.13 10.12 10.11 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 Standard deviation Return -0.65 12 (12 =0.00 0.65 12 B. FE(R) 0.18 +0.17 0.16 EEE F0.15 D D D 0.14 -0.13 0.12 Up BB 0.11 0.01 0.07 0.08 0.02 0.03 0.04 0.05 0.06 Standard Deviation of Return 12 -0.65 12=0.00 -- 0.65 12 FE(R) 0.18 Fo.17 EEE 10.16 D D D +0.15 (c ! -0.14 0.13 99 B dB 0.12 0.11 0.01 0.02 0.03 0.04 0.05 0.09.0.02 0.08. Standard Deviation of Return) =0.65 12 0.65 12=0.00 12 D. FE(R) 0.18 0.17 EEE -0.16 D D 10.15 F0.14 0.13 BBB 0.12 0.11 0.01 0.02. 0.03 0.04 0.05 0.06 Standard Deviation of Return(0) 0:07:28 =0.65 12 -0.00 12 0.65