Help on Python code

Code needs to pass assertion tests

def derivate_approx(f, x, varval, delta=0.0001):

"""Computes the derivative of f with respect to x, for a given delta,

using the (f(x + delta) - f(x)) / delta method. """

# This is f(x)

f_x = compute(f, varval=varval)

varval_delta = dict(varval)

varval_delta[x] += delta

# This is f(x + delta)

f_x_plus_delta = compute(f, varval=varval_delta)

return (f_x_plus_delta - f_x) / delta

def similar(x, y, epsilon):

if x

# If they are negative, max and min play opposite roles.

return similar(-x, -y, epsilon)

if abs(x - y)

return True

else:

return max(x, y) / (min(x, y) + epsilon)

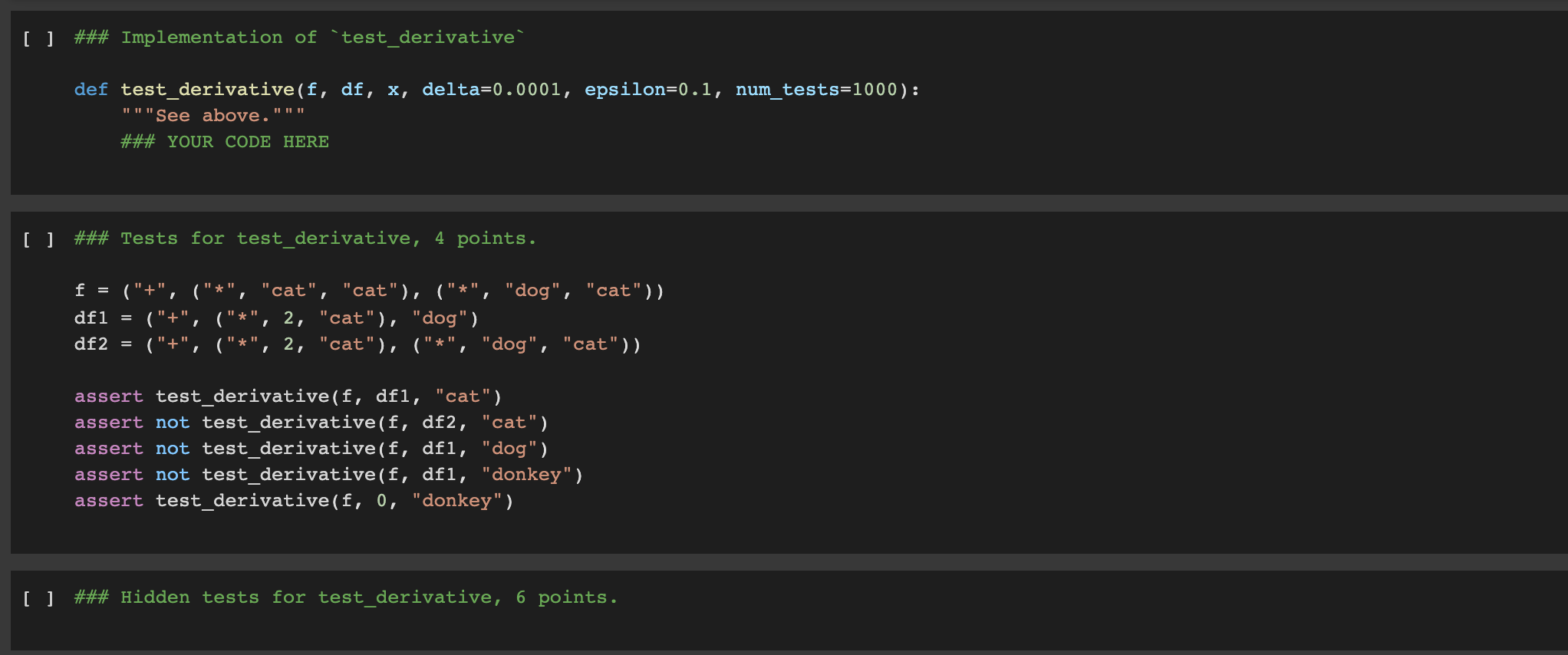
### Implementation of `test_derivative`

def test_derivative(f, df, x, delta=0.0001, epsilon=0.1, num_tests=1000):

"""See above."""

### YOUR CODE HERE

### Tests for test_derivative, 4 points.

f = ("+", ("*", "cat", "cat"), ("*", "dog", "cat"))

df1 = ("+", ("*", 2, "cat"), "dog")

df2 = ("+", ("*", 2, "cat"), ("*", "dog", "cat"))

assert test_derivative(f, df1, "cat")

assert not test_derivative(f, df2, "cat")

assert not test_derivative(f, df1, "dog")

assert not test_derivative(f, df1, "donkey")

assert test_derivative(f, 0, "donkey")

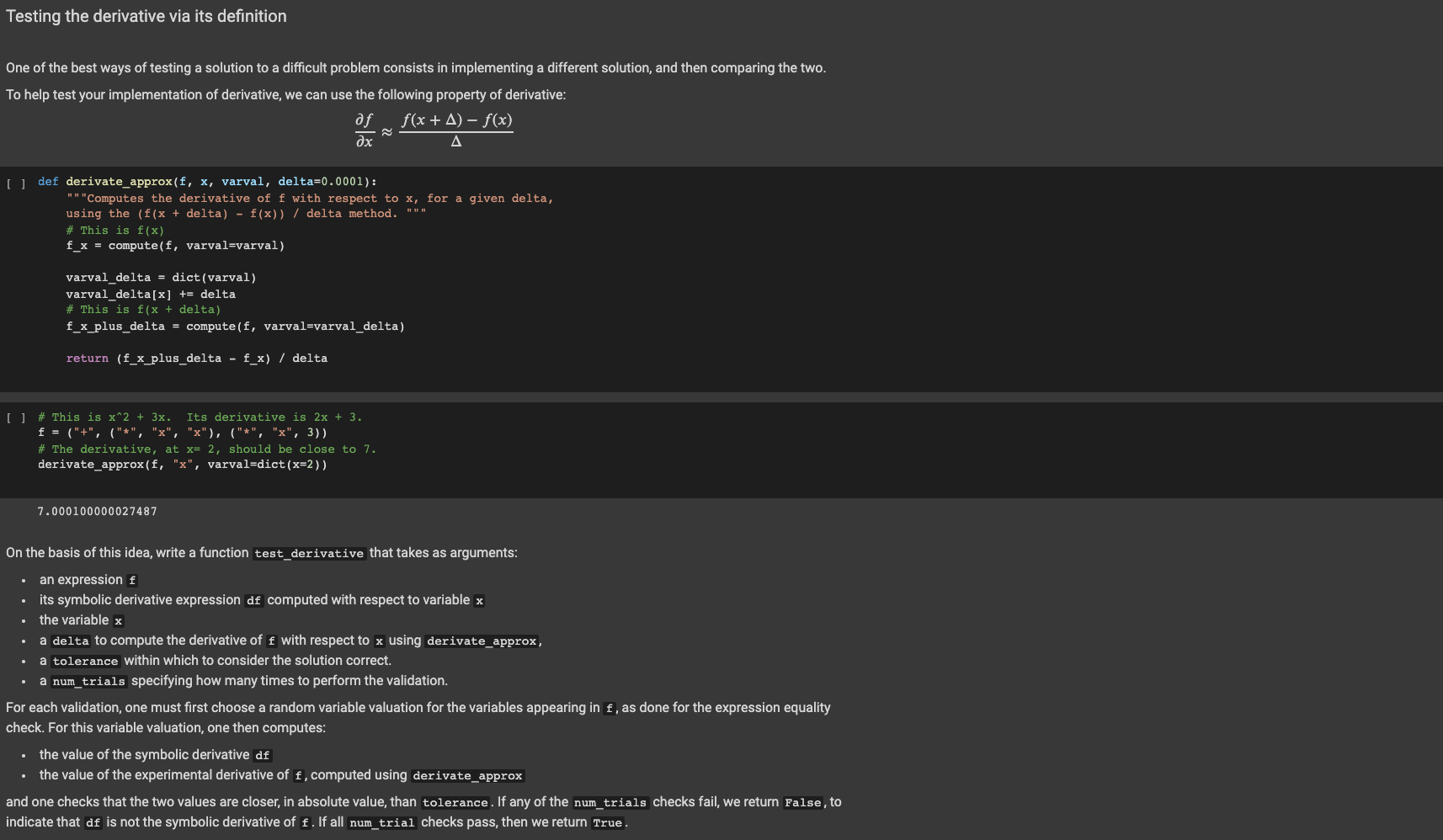
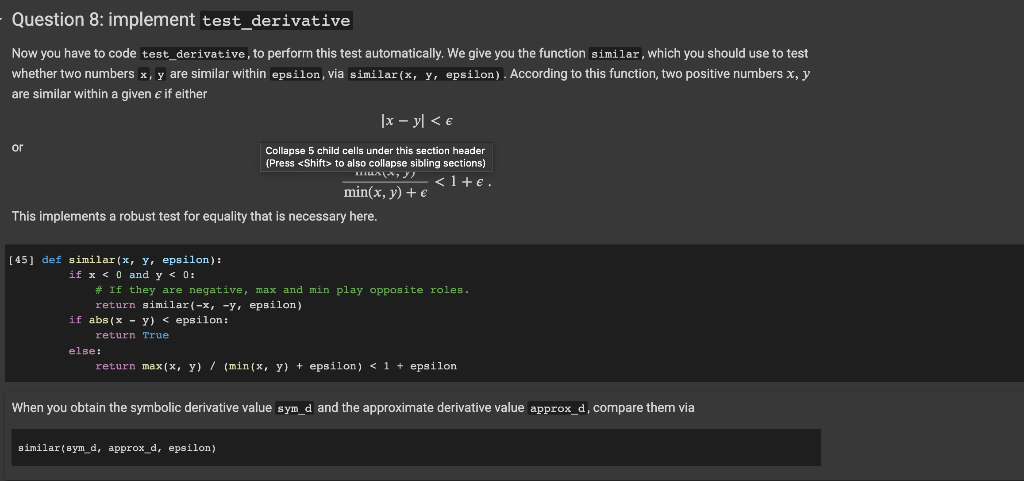
Testing the derivative via its definition One of the best ways of testing a solution to a difficult problem consists in implementing a different solution, and then comparing the two. To help test your implementation of derivative, we can use the following property of derivative: of f(x + A) f(x) [] def derivate_approx(f, x, varval, delta=0.0001): "" "Computes the derivative of f with respect to x, for a given delta, using the (f(x + delta) - f(x)) / delta method. # This is f(x) f_x = compute(f, varval=varval) varval_delta = dict(varval) varval_delta[x] += delta # This is f(x + delta) f_x_plus_delta = compute(f, varval=varval_delta) return (f_x_plus_delta - f_x) / delta [] # This is x^2 + 3x. Its derivative is 2x + 3. f = ("+", ("*", "x", "x"), ("*", "x", 3)) # The derivative, at x= 2, should be close to 7. derivate_approx(f, "x", varval=dict(x=2)) 7.000100000027487 On the basis of this idea, write a function test derivative that takes as arguments: an expression f its symbolic derivative expression df computed with respect to variable x the variable x a delta to compute the derivative of f with respect to x using derivate_approx, a tolerance within which to consider the solution correct. a num_trials specifying how many times to perform the validation. For each validation, one must first choose a random variable valuation for the variables appearing in f, as done for the expression equality check. For this variable valuation, one then computes: the value of the symbolic derivative df the value of the experimental derivative of f, computed using derivate_approx and one checks that the two values are closer, in absolute value, than tolerance. If any of the num_trials checks fail, we return false, to indicate that df is not the symbolic derivative of f. If all num_trial checks pass, then we return True. Question 8: implement test_derivative Now you have to code test_derivative, to perform this test automatically. We give you the function similar, which you should use to test whether two numbers x, y are similar within epsilon, via similar(x, y, epsilon). According to this function, two positive numbers x, y are similar within a given e if either |x y to also collapse sibling sections) to also collapse sibling sections)