Question: I'm following the attached lecture notes for proving Convergence almost everywhere implies convergence in measure with Egoroff's theorem. Convergence almost everywhere implies convergence in mea-
I'm following the attached lecture notes for proving "Convergence almost everywhere implies convergence in measure" with Egoroff's theorem.
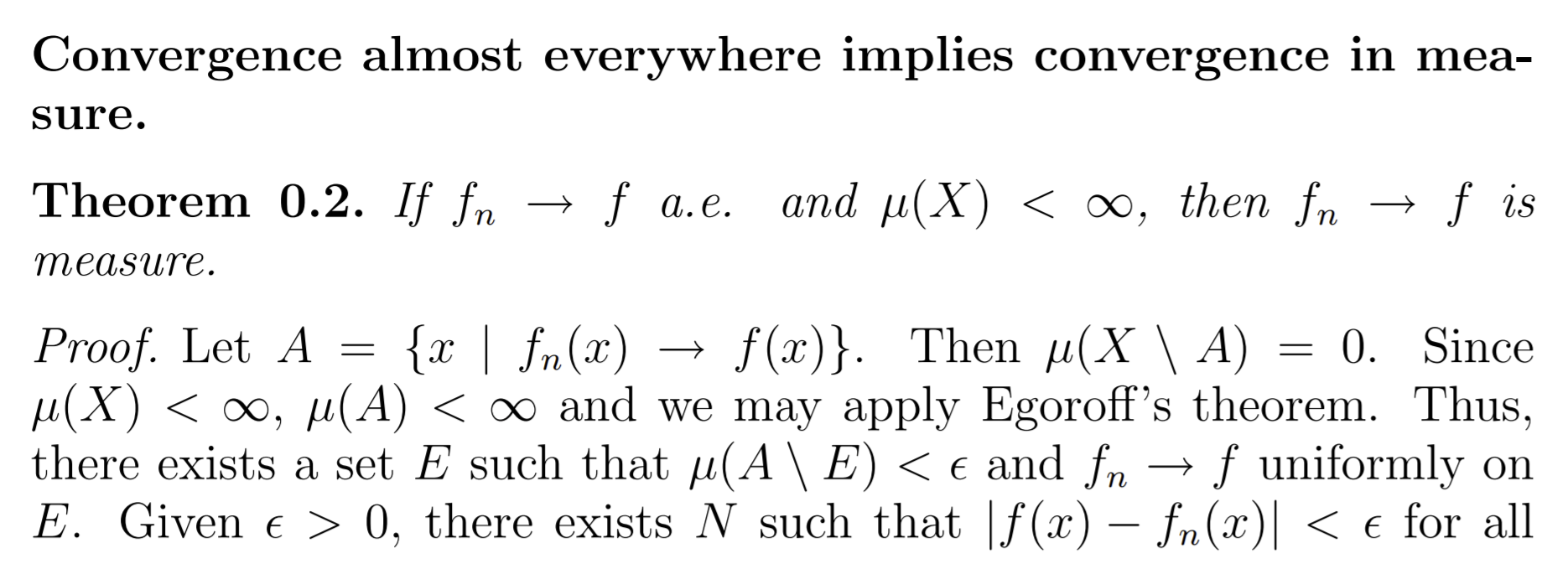
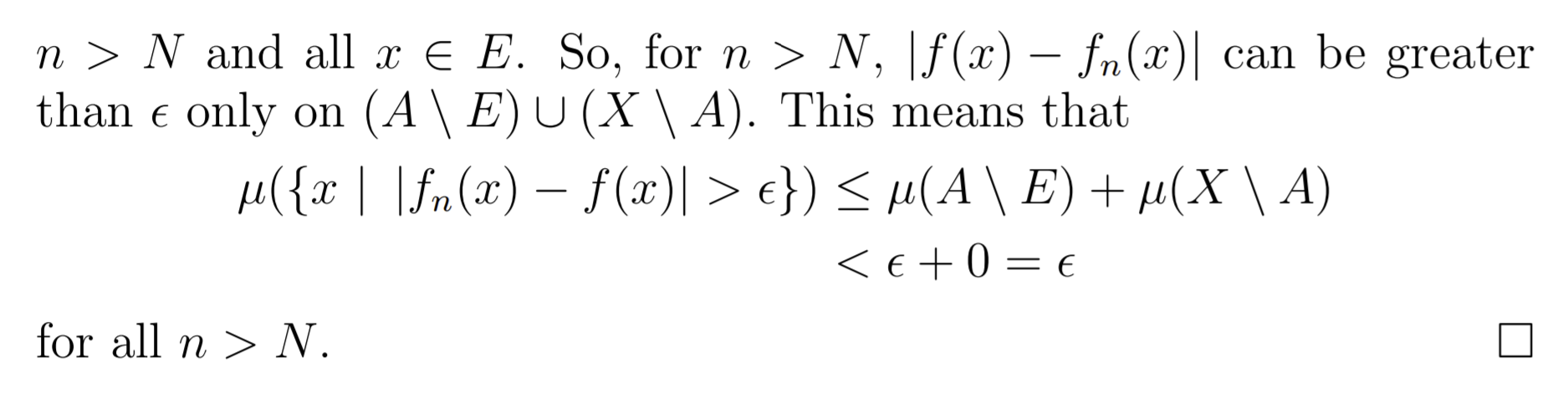
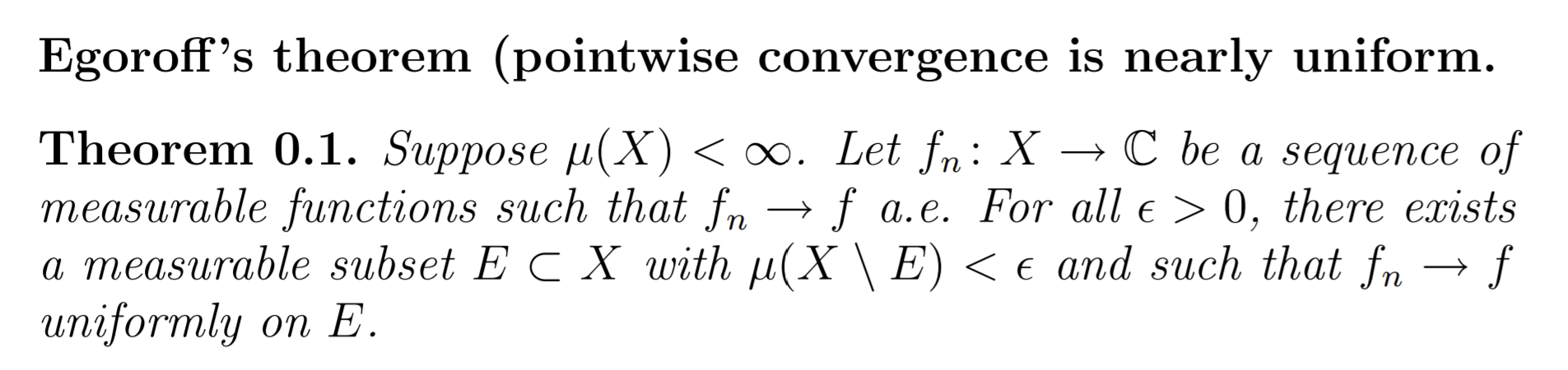
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


