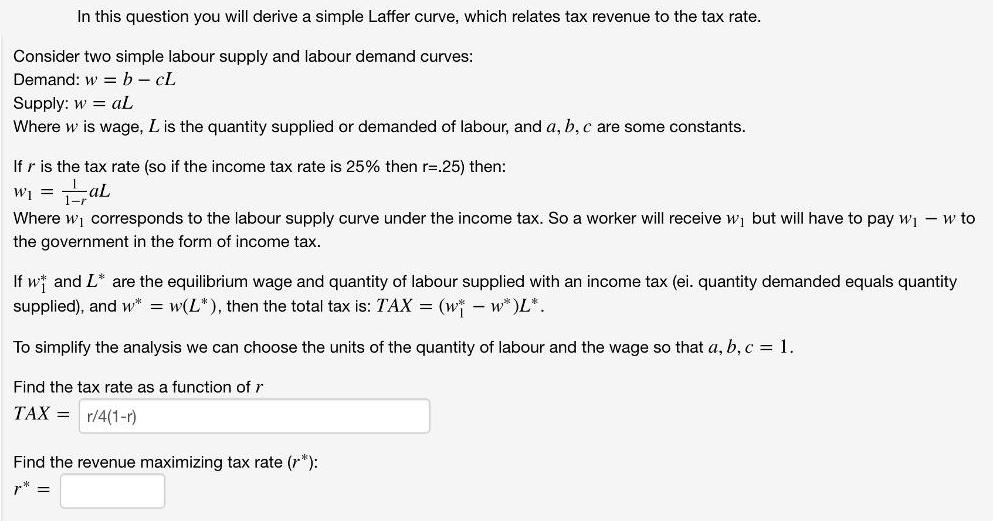
In this question you will derive a simple Laffer curve, which relates tax revenue to the tax rate. Consider two simple labour supply and labour demand curves: Demand: w = b cL Supply: w = al Where w is wage, L is the quantity supplied or demanded of labour, and a, b, c are some constants. If r is the tax rate (so if the income tax rate is 25% then r=.25) then: Wi = aL Where wi corresponds to the labour supply curve under the income tax. So a worker will receive w, but will have to pay wj w to the government in the form of income tax. If w and L* are the equilibrium wage and quantity of labour supplied with an income tax (ei. quantity demanded equals quantity supplied), and w* = w(L*), then the total tax is: TAX = (w* - w* )L*. To simplify the analysis we can choose the units of the quantity of labour and the wage so that a, b, c = 1. Find the tax rate as a function of r TAX = r/4(1-r) Find the revenue maximizing rate (r*): r* =