Question: Let (S, d) be a dissimilarity space. Prove that d is an quasi-ultrametric 6 . Let ( S, d ) be a dissimilarity space .

Let (S, d) be a dissimilarity space. Prove that d is an quasi-ultrametric

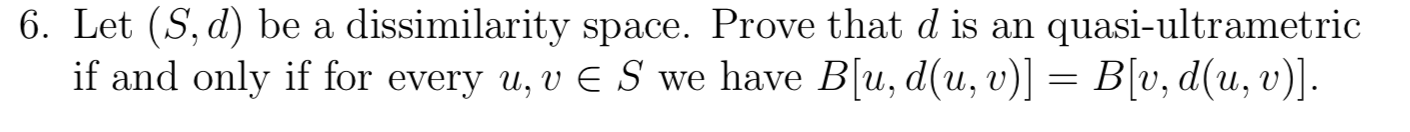
6 . Let ( S, d ) be a dissimilarity space . Prove that d is an quasi - ultrametric if and only if for every u , u E S' we have B \\ u , d ( U , V) ] = B [ V , d ( U , V) ]

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

EXAM II: PRACTICE SHEET (1) All the HW problems! (2) (a) Let (X, d) be a metric space. Prove that the closed neighborhood N r (x) = {y X : d(x, y) r} is a closed set. (b) Let (Rn , d) with the...

Solve Supplementary Problems COMPLETE METRIC SPACES 22. Let (X, d) be a metric space and let e be the metric on X defined by e(a, b) = min {1, d(a, b)). Show that (a,) is a Cauchy sequence in (X, d)...

It should be step by step. Ur help will be highly appreciated. It is a topology in pure mathematics. 1. Answers to the questions should be fully and clearly explained QUESTION ONE a) Define carefully...

Let (M,d) be a metric space and let AC M be non-empty. Prove that the following are equivalent: (1) A is bounded. (2) There exists a D20 so that, for every a, b A, we have d(a, b) D. Problem 5: Let...

5. (a) Let (X, d) be a metric space. Consider the metric space (XXX, 61*) where d*((m, y), (u, v)) = max{d(x, u), d(y, 11)} (see Homework 5 Problem 1.) Show that the original metric d : X X X > IR is...

Name: \"Cl/V\" \"V V' "' \""J Note: Turn in as many as four solutions, but only the' three highest scores will be considered. GOOD LUCK! 1. Let A be an uncountable set, and let B be a countable set....

3. Let (X, D) Be A Metric Space. Define D: XxXR By D(X, Y) = Min(1, D(X, Y). (A) Prove That D Is A Metric On X. (B) Let (Un)Ren Be A Sequence In X. Further Let : E X. Prove That X = D-Lim , If And...

Let (X, d) be a metric space and suppose r> 0 and (Pn) is a sequence from X such that d(pn, Pm) r for nm. Show E = {pn: ne N} is closed. chatgpt to scott: To show that E is closed, we must prove that...

Exercise 6. Let (X, d) be a metric space. Given E C X, let E be the set of interior points of E. (The set E is called the interior of E.) (a) If GCE is open, prove that G C E. (b) Prove that E is an...

1. Generate a matrix containing 5000 samples from the Weibull distribution with a = 1 and 3 = 2, each of size n = 100. Compute the 500 means using the apply function and store it in x2matmn. Call...

How many electrons should be removed from an initially uncharged spherical conductor of radius 0.300 m to produce a potential of 7.50 kV at the surface?

The most important improvement in climate models that allows better forecasting is arguably increased speed of calculation

A company issues 1,050 shares of its common stock for $33,600 cash. Prepare journal entries to record this event under each of the following separate situations.