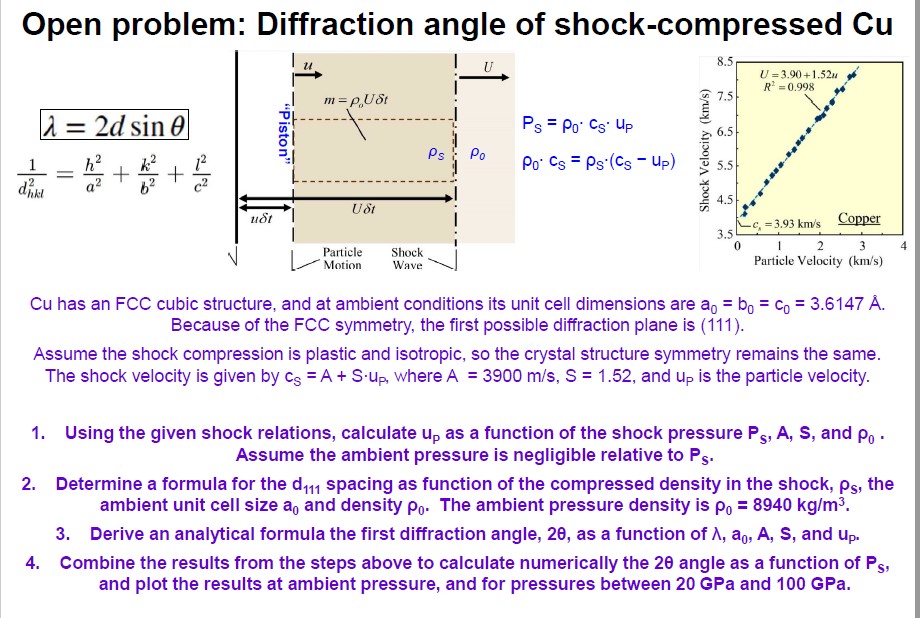
Open problem: Diffraction angle of shock$-$compressed Cu

$\backslash$lambda $=2$dsin$\backslash$theta

$(1)/($d$\_($hkl$)^(2))=($h$^(2))/($a$^(2))+($k$^(2))/($b$^(2))+($l$^(2))/($c$^(2))$

P$\_($S$)=\backslash$rho $\_(0)*$c$\_($S$)*$u$\_($P$)$

$\backslash$rho $\_(0)*$c$\_($S$)=\backslash$rho $\_($S$)*($c$\_($S$)-$u$\_($P$))$

Cu has an FCC cubic structure, and at ambient conditions its unit cell dimensions are a$\_(0)=$b$\_(0)=$c$\_(0)=3\mathrm{.}6147\backslash$angstrom $.$

Because of the FCC symmetry, the first possible diffraction plane is $(111).$

Assume the shock compression is plastic and isotropic, so the crystal structure symmetry remains the same.

The shock velocity is given by c$\_($S$)=$A$+$S$*$u$\_($p$),$ where A$=3900($m$)/($s$),$S$=1\mathrm{.}52,$ and u$\_($p$)$ is the particle velocity.

Using the given shock relations, calculate u$\_($p$)$ as a function of the shock pressure P$\_($S$),$A$,$S$,$ and $\backslash$rho $\_(0).$

Assume the ambient pressure is negligible relative to P$\_($S$).$

Determine a formula for the d$\_(111)$ spacing as function of the compressed density in the shock, $\backslash$rho $\_($s$),$ the

ambient unit cell size a$\_(0)$ and density $\backslash$rho $\_(0).$ The ambient pressure density is $\backslash$rho $\_(0)=8940$k$($g$)/($m$^(3)).$

Derive an analytical formula the first diffraction angle, $2\backslash$theta $,$ as a function of $\backslash$lambda $,$a$\_(0),$A$,$S$,$ and u$\_($p$).$

Combine the results from the steps above to calculate numerically the $2\backslash$theta angle as a function of P$\_($S$),$

and plot the results at ambient pressure, and for pressures between $20$ GPa and $100$ GPa $.$