Please EXPLAIN and solve EACH/ALL part(s) in Question #6!

DOUBLE CHECK YOUR WORK AND ANSWER(S).

PLEASE NEATLY SHOW ALL WORK, EXPLANATIONS, & CALCULATIONS STEP-BY-STEP USING PEN AND PAPER! I AM NEW TO CHEMISTRY! I AM A COMPLETE NEWBIE!

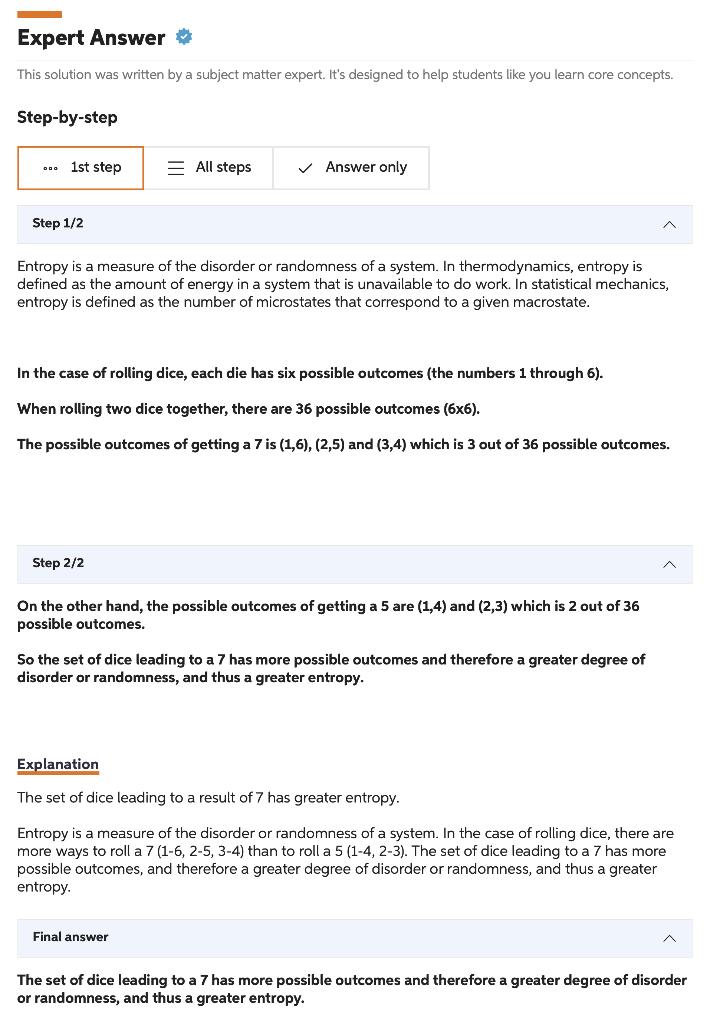
5. Which system has the greater entropy? The set of dice leading to a result of 7 or the set of dice leading to a result of 5 ? Type your answer here. This solution was written by a subject matter expert. It's designed to help students like you learn core concepts. Step-by-step Step 1/2 Entropy is a measure of the disorder or randomness of a system. In thermodynamics, entropy is defined as the amount of energy in a system that is unavailable to do work. In statistical mechanics, entropy is defined as the number of microstates that correspond to a given macrostate. In the case of rolling dice, each die has six possible outcomes (the numbers 1 through 6). When rolling two dice together, there are 36 possible outcomes (66). The possible outcomes of getting a 7 is (1,6),(2,5) and (3,4) which is 3 out of 36 possible outcomes. Step 2/2 On the other hand, the possible outcomes of getting a 5 are (1,4) and (2,3) which is 2 out of 36 possible outcomes. So the set of dice leading to a 7 has more possible outcomes and therefore a greater degree of disorder or randomness, and thus a greater entropy. Explanation The set of dice leading to a result of 7 has greater entropy. Entropy is a measure of the disorder or randomness of a system. In the case of rolling dice, there are more ways to roll a 7(16,25,34) than to roll a 5(14,23). The set of dice leading to a 7 has more possible outcomes, and therefore a greater degree of disorder or randomness, and thus a greater entropy. Final answer The set of dice leading to a 7 has more possible outcomes and therefore a greater degree of disorder or randomness, and thus a greater entropy. Part 2 - Boltzmann's Equation for Entropy Ludwig Boltzmann developed an equation to calculate the entropy of a system: S=klnW where S is entropy, W is the number of microstates (possible ways to arrange the system), and k is the Boltzmann constant (1.381023J/K) 6. Calculate the change in entropy (S) for the system as it "moves" from the result of 5 from the two dice to the result of 7 for the two dice. Remember, when we calculate a change in a property as final state minus initial state, SfinalSinitial. Insert an image of your work here