please use python and # to explain what you are doing. please be aware there are hidden test

these pictures are all a part of one question.

you have to write code that runs the test AND hidden test perfectly. the code needed is for the test at the end that are labeled un green (ex. 5pts, 10pts) . the code should run the hidden test. I have reuploaded the photos.

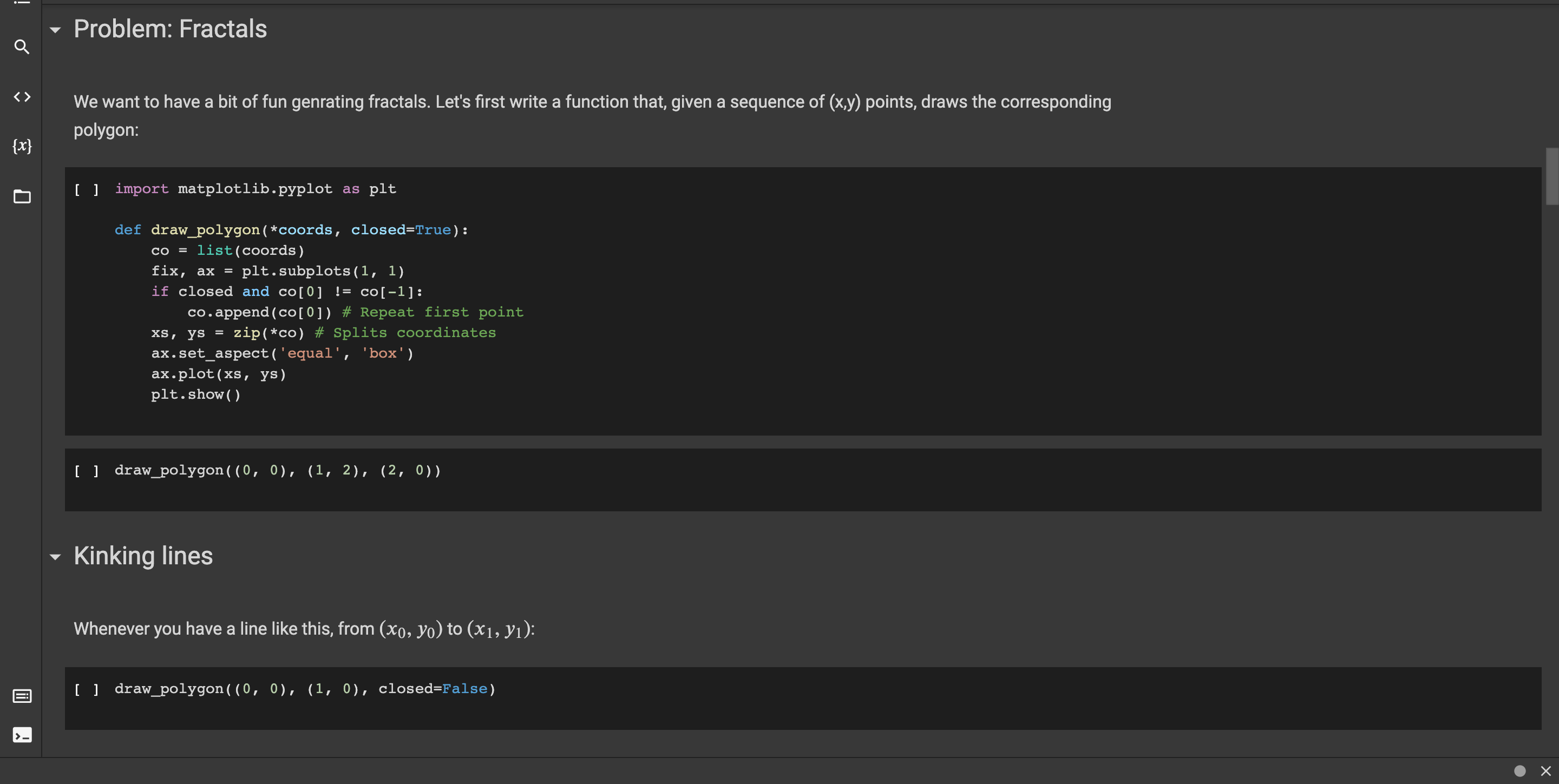
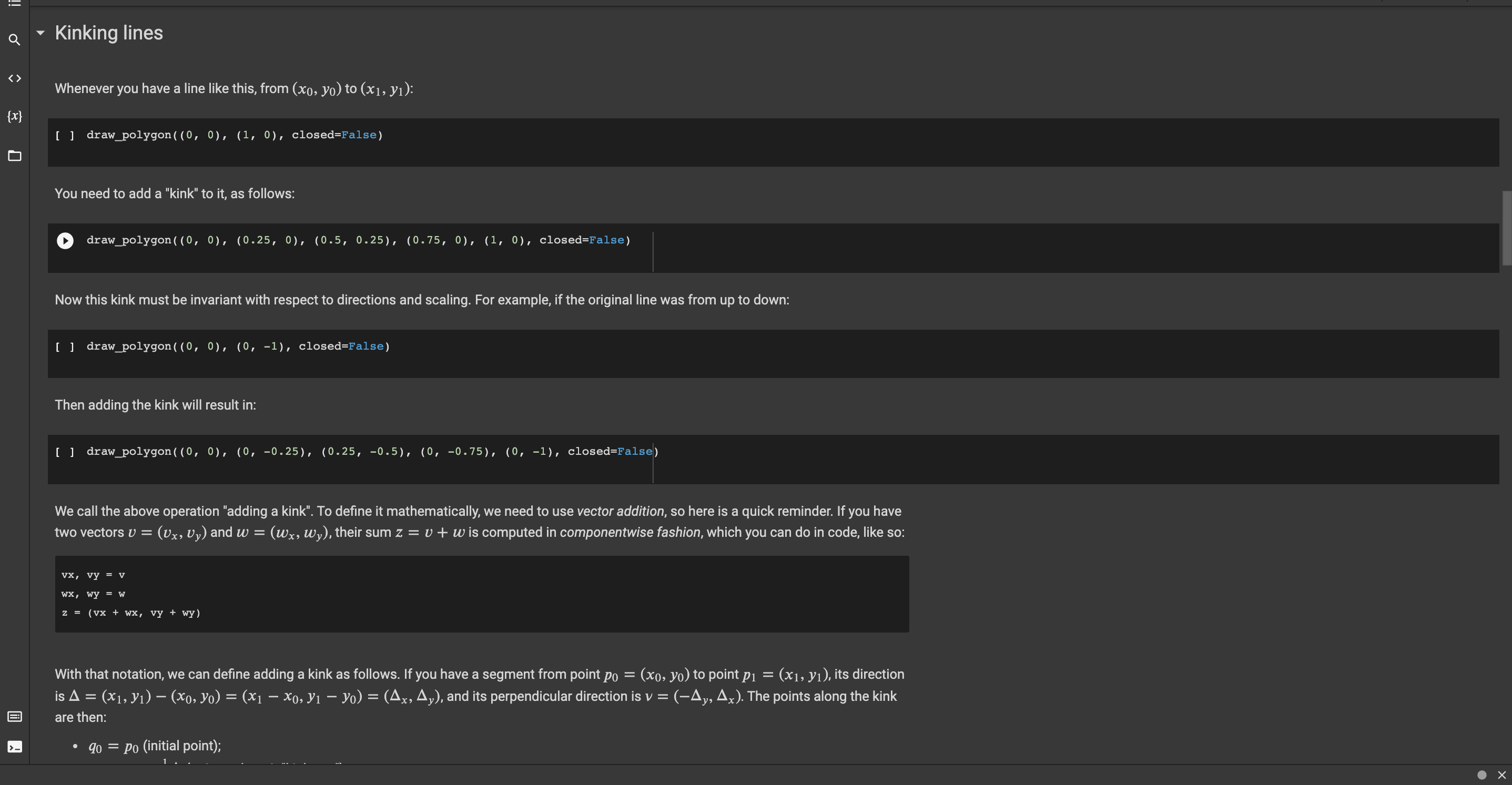
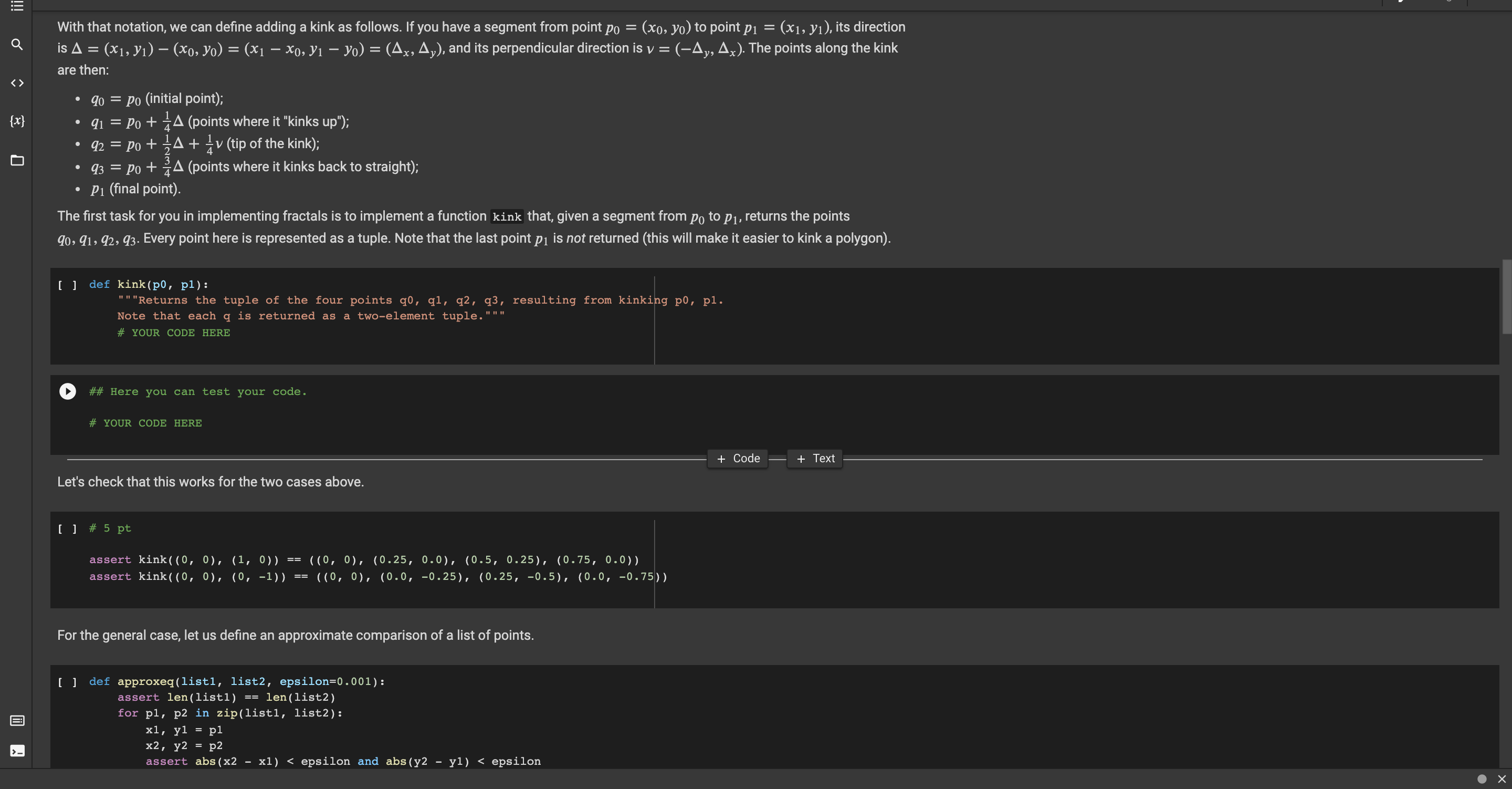
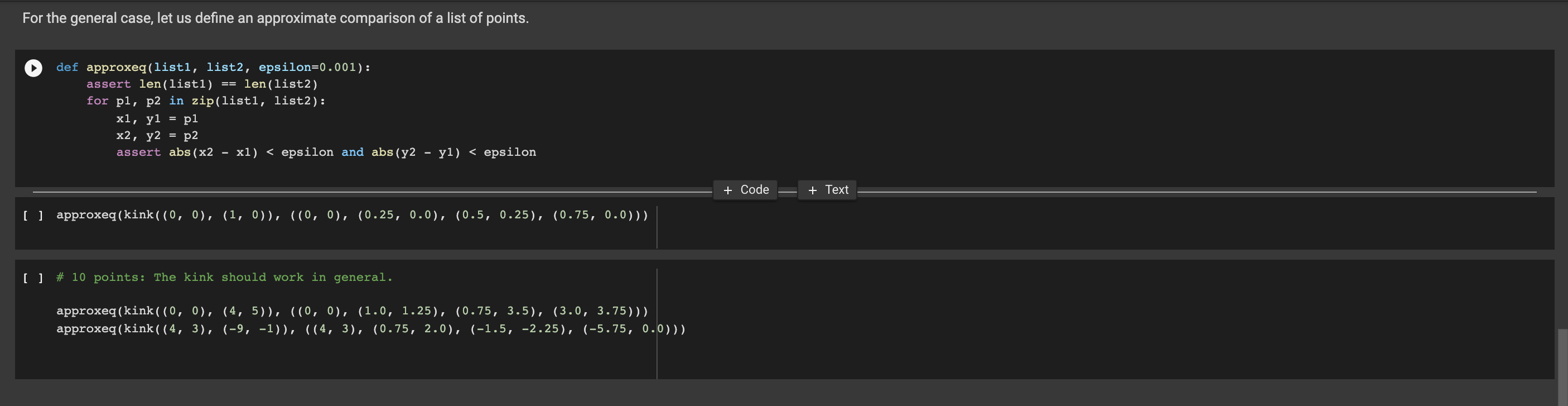
.- Problem: Fractals Q We want to have a bit of fun genrating fractals. Let's first write a function that, given a sequence of (x,y) points, draws the corresponding polygon: {x} o [] import matplotlib.pyplot as plt CO = = def draw_polygon (*coords, closed=True): list(coords) fix, ax plt.subplots(1, 1) if closed and co[0] != co[-1]: co.append(Co[0]) # Repeat first point Xs, ys zip(*co) # Splits coordinates ax.set_aspect('equal', 'box') ax.plot(xs, ys) plt.show() [ ] draw_polygon((0, 0), (1, 2), (2, 0)) Kinking lines Whenever you have a line like this, from (xo, yo) to (x1, y): [ ] draw_polygon((0, 0), (1, 0), closed=False) > ii a Kinking lines Whenever you have a line like this, from (x0, yo) to (x1, y): {x} ( draw_polygon((0, 0), (1, 0), closed=False) You need to add a "kink" to it, as follows: draw_polygon ((0, 0), (0.25, 0), (0.5, 0.25), (0.75, 0), (1, 0), closed=False) Now this kink must be invariant with respect to directions and scaling. For example, if the original line was from up to down: I draw_polygon((0, 0), (0, -1), closed=False) Then adding the kink will result in: I draw_polygon ((0, 0), (0, -0.25), (0.25, -0.5), (0, -0.75), (0, -1), closed=False) We call the above operation "adding a kink". To define it mathematically, we need to use vector addition, so here is a quick reminder. If you have two vectors v = (Ux, Vy) and w = (Wx, wy), their sum z = v + w is computed in componentwise fashion, which you can do in code, like so: vx, vy = V wx, wy = w z = (vx + wx, vy + wy) = With that notation, we can define adding a kink as follows. If you have a segment from point po (xo, yo) to point p1 = (x1, y), its direction is A (x1, y) (xo, Yo) = (x1 Xo, Y1 yo) = (4x, Ay), and its perpendicular direction is v = (-Ay, Ax). The points along the kink are then: = = = 9o = po (initial point); iii Q With that notation, we can define adding a kink as follows. If you have a segment from point po = = (xo, yo) to point p1 = (x1, y), its direction is A = (x1, y1) (xo, Yo) = (x1 Xo, Y1 yo) = (4x, Ay), and its perpendicular direction is v = (-Ay, Ax). The points along the kink are then: = {x} . . 90 = po (initial point); 91 = Po + 44 (points where it "kinks up"); 92 = po + {4 + 4v (tip of the kink); 93 = po + A (points where it kinks back to straight); P1 (final point). The first task for you in implementing fractals is to implement a function kink that, given a segment from po to P1, returns the points 90, 91, 92, 93. Every point here is represented as a tuple. Note that the last point p1 is not returned (this will make it easier to kink a polygon). a [] def kink(po, pl): " "Returns the tuple of the four points qo, q1, 92, 93, resulting from kinking po, pl. Note that each q is returned as a two-element tuple.""". # YOUR CODE HERE ## Here you can test your code. # YOUR CODE HERE + Code + Text Let's check that this works for the two cases above. [] # 5 pt assert kink((0, 0), (1, 0)) == ((0, 0), (0.25, 0.0), (0.5, 0.25), (0.75, 0.0)) assert kink((0, 0), (0, -1)) ((0, 0), (0.0, -0.25), (0.25, -0.5), (0.0, -0.75)) For the general case, let us define an approximate comparison of a list of points. [] == def approxeq(listi, list2, epsilon=0.001): assert len(listi) len(list2) for pl, p2 in zip(listi, list2): x1, y1 = pl x2, y2 = p2 assert abs(x2 xl)