Question: Question) Give the code for the following functions where the class below is given: a) def derivate_leaf(e, x), b) def derivate(e, x), c) def test_derivative(f,
Question) Give the code for the following functions where the class below is given: a) def derivate_leaf(e, x), b) def derivate(e, x), c) def test_derivative(f, df, x, delta=0.0001, epsilon=0.1, num_tests=1000), and d) def apply_distributive(e). It must follow the exact parameters and pass the tests assigned to each function below. Insert code where it says, "YOUR CODE HERE."

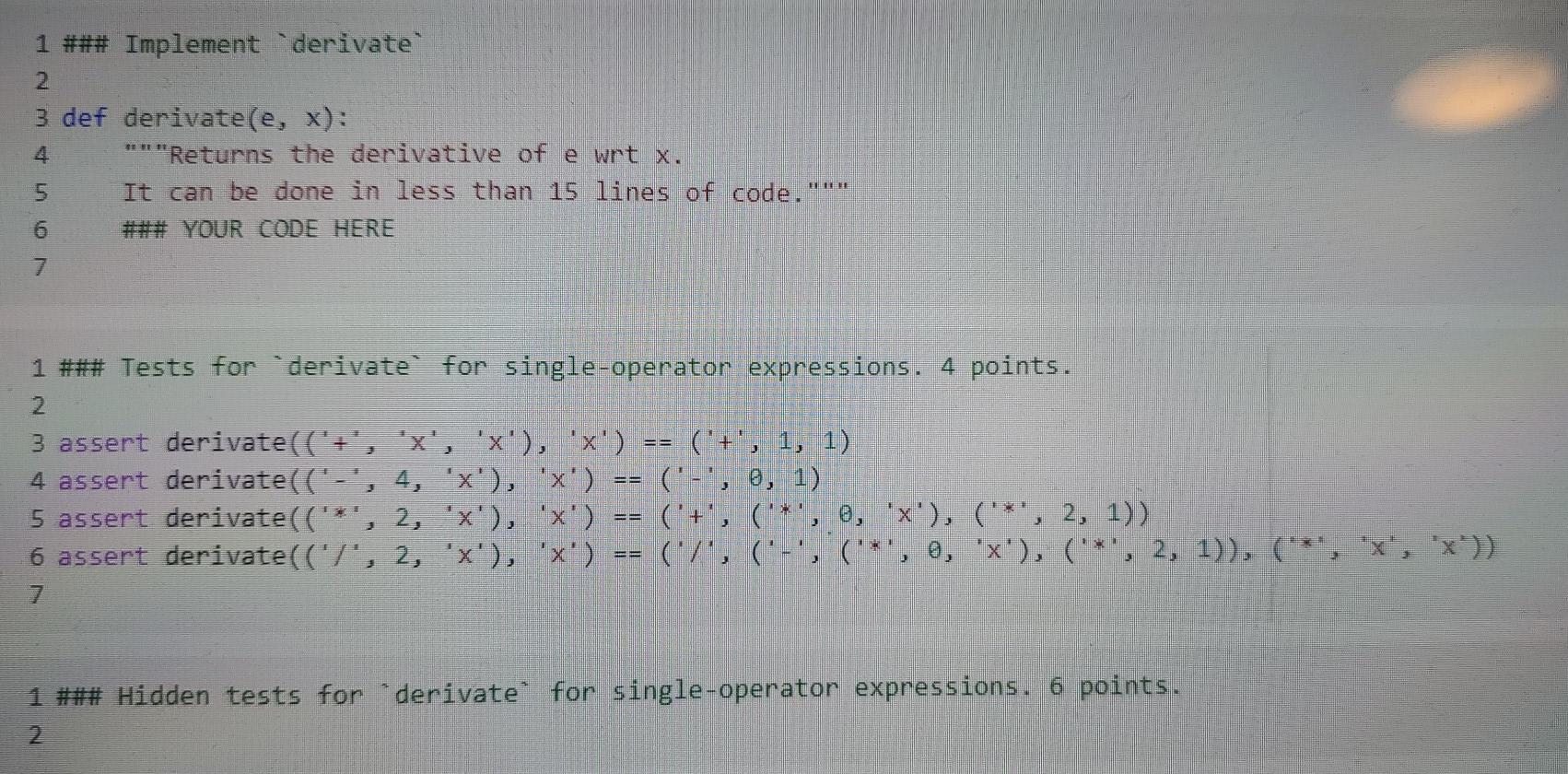
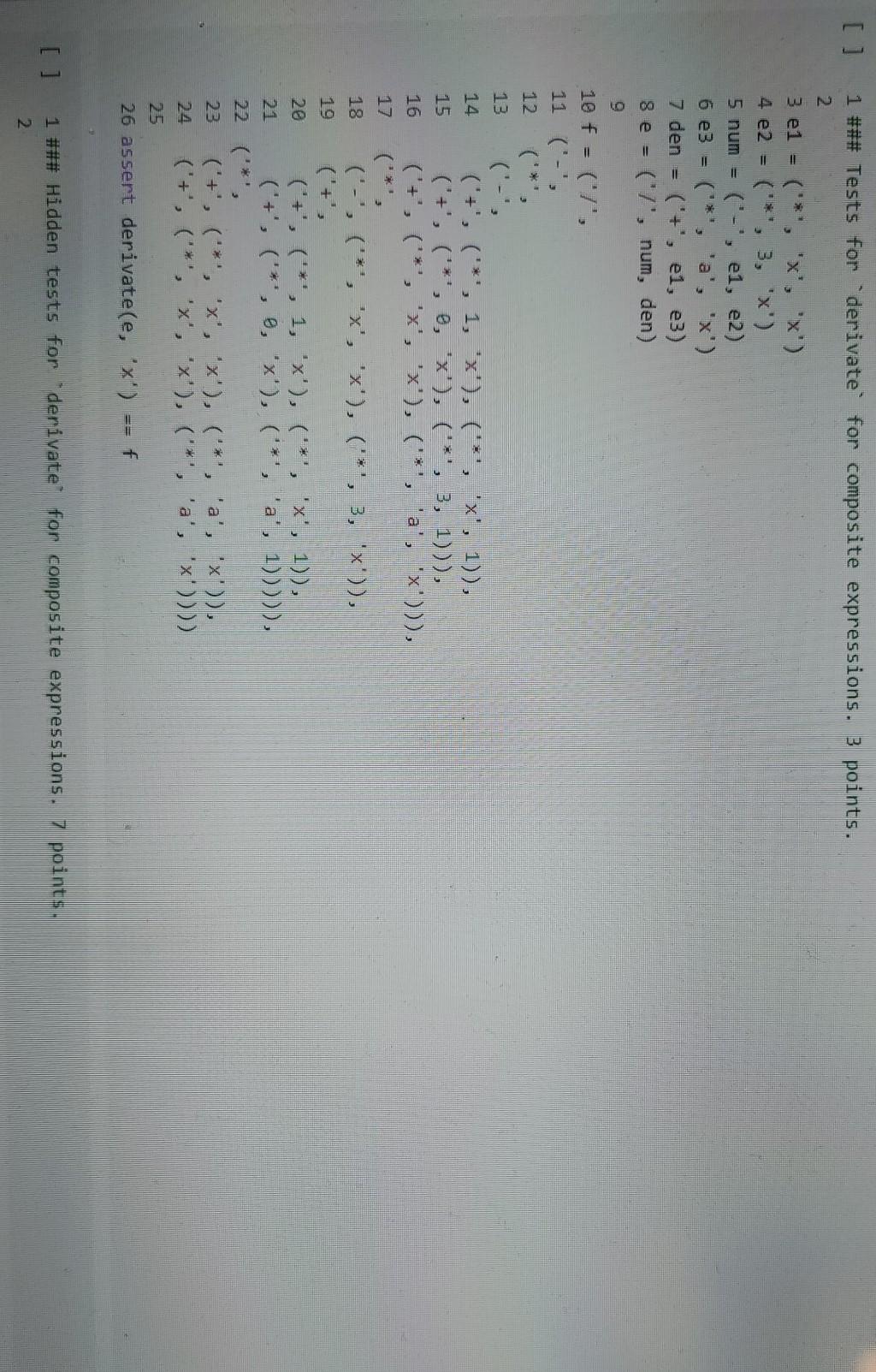
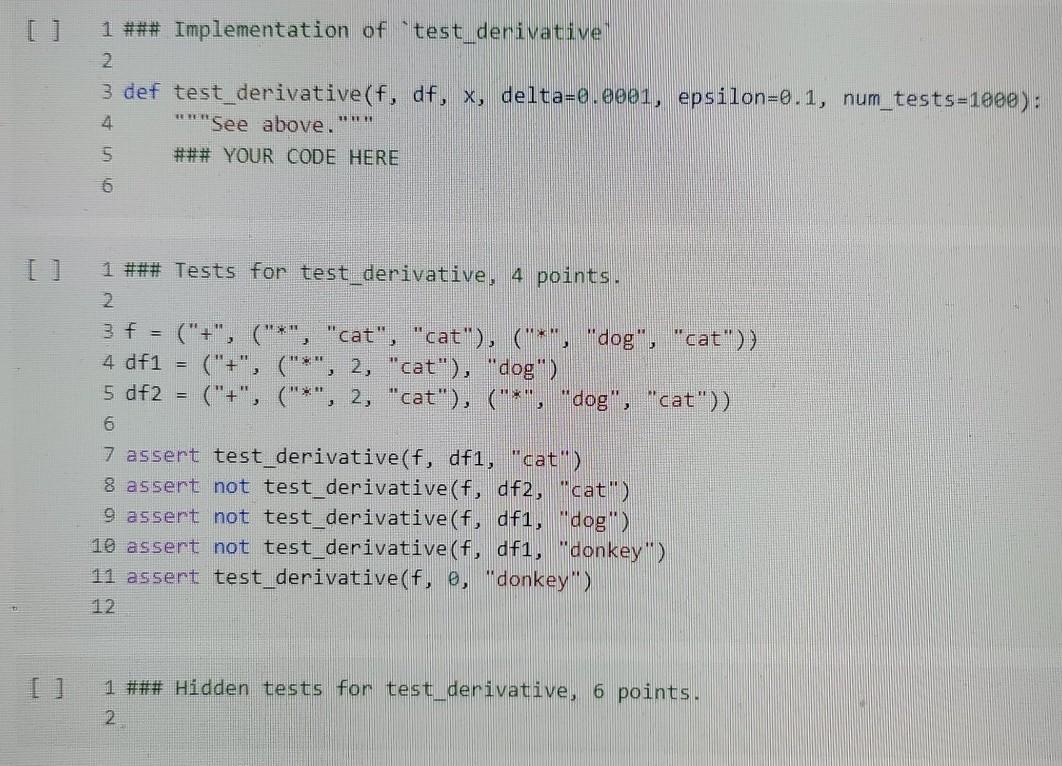
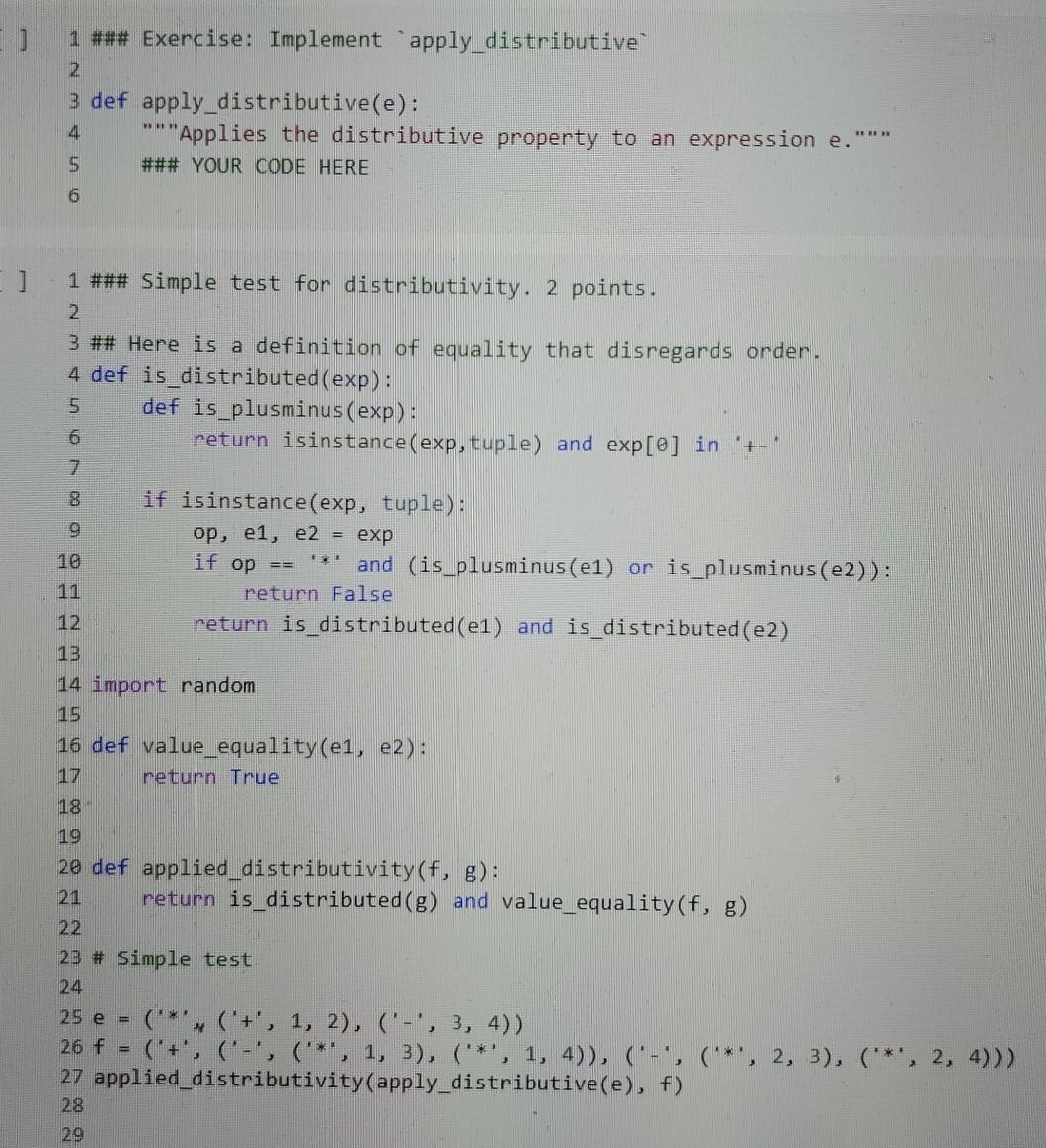
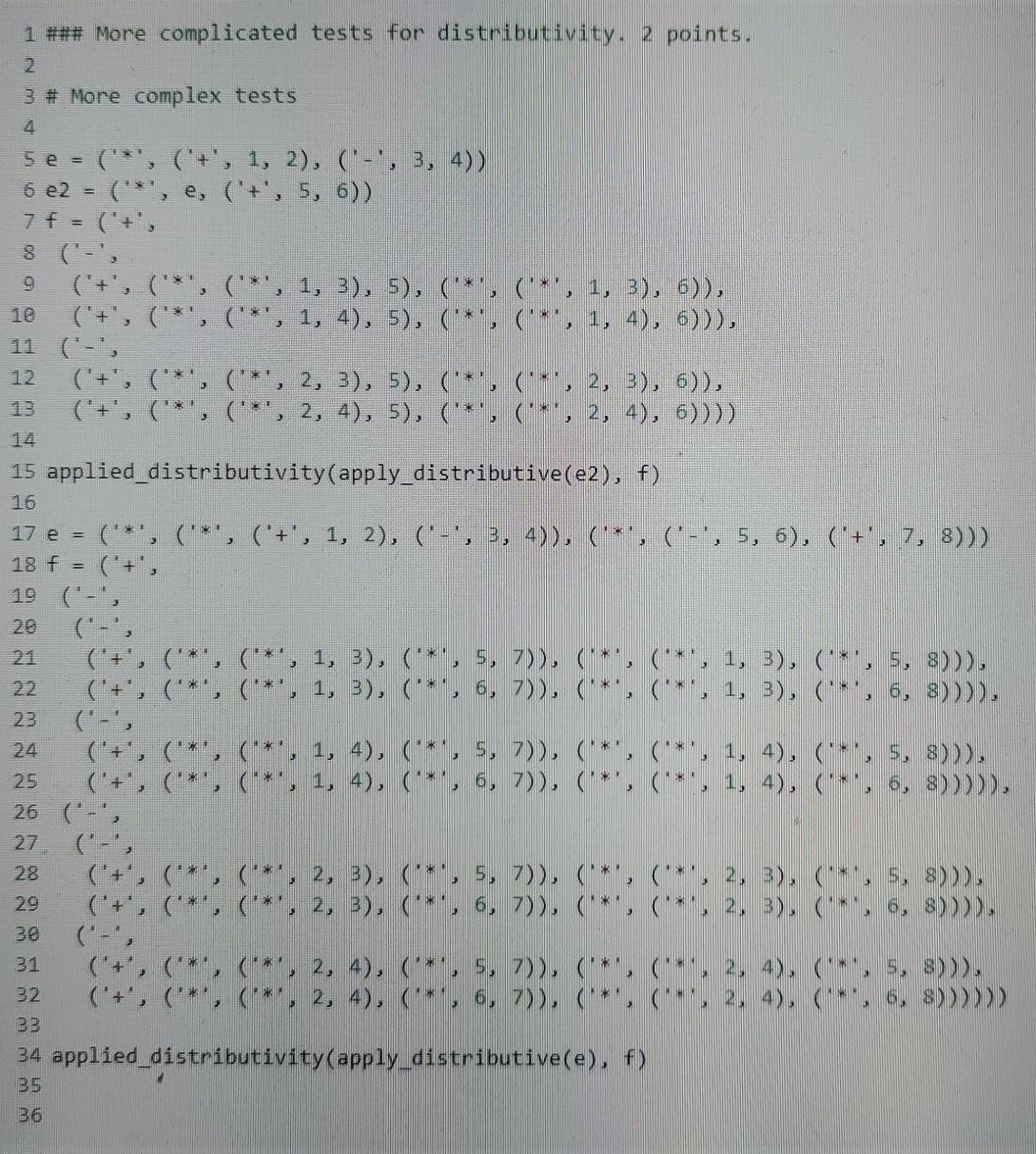
4 1 ### Derivation of a leaf expression 2. 3 def derivate_leaf(e, x): ***"This function takes as input an expression e and a variable x, 5 and returns the symbolic derivative of e wrt. X, as an expression." 6 ### YOUR CODE HERE 7 1 ## Derivative of a leaf expression. 2 points. 2. == 1 3 assert derivate_leaf("x", "x") 4 assert derivate_leaf("x", "y") 5 assert derivate_leaf ("y", "z" 6 assert derivate_leaf(4, "x") @ 7. 1 ## Hidden tests for derivative of a leaf expression. 3 points. 2 1 ### Implement "derivate 2. 3 def derivate(e, x): ** "Returns the derivative of e wrt x. 5 It can be done in less than 15 lines of code. 6 ### YOUR CODE HERE EFE 7 1 ### Tests for derivate for single-operator expressions. 4 points. 3 assert derivate(('+', 'x', 'x'), 'x') == ('+', 1, 1) 4 assert derivate(('-', 4, 'x'), 'x') == ('-', 0, 1) 5 assert derivate(('*', 2, 'x'), 'x') ('+', ('*', 0, 'x'), ('*', 2, 1)) 6 assert derivate(('/', 2, 'x'), 'x') == ('7', ('-', ('*', 0, 'x'), ('*', 2, 1)), ('*', 'x', 'x')) 1 ### Hidden tests for 'derivate for single-operator expressions. 6 points. [] 1 ### Tests for derivate for composite expressions. 3 points. 2 3 e1 = ('*', 'x', 'x') 4 e2 = ('*', 3, 'x') 5 num = ('-', ei, e2) 6 e3 = (*', 'a', 'x') 7 den = ('+', el, e3) 8 e = ('7', num, den) 9 10 f = ('7', 11 ('-', 12 13 14 15 16 ('+', ('*', 1, 'x'), ('*', 'x', 1)), ('+', ('*', 0, 'x'), ('*', 3, 1))), ('+', ("*', 'x', 'x'), ('*', 'a', 'x'))), 18 ('-', ('*', 'x', 'x'), ('*', 3, 'x')), 19 28 ('+', ('*', 1, 'x'), ('*', 'x', 1)), ('+', ('*', 0, 'x'), ('*', 'a', 1))))), 22 ('*', 23 ('+', ('*', 'x', 'x'), ('*', 'a', 'x')), 24 ('+', ("*', 'x', 'x'), ('*', 'a', 'x')))) 25 26 assert derivate(e, 'x') == f [ ] 1 ### Hidden tests for "derivate for composite expressions. 7 points. 2 1 ### Implementation of test_derivative 2 2 3 def test_derivative(f, df, x, delta=0.8ee1, epsilon=0.1, num_tests=1808): See above." 5. ### YOUR CODE HERE 4. 1 ### Tests for test_derivative, 4 points. 2 3 f = ("+", ("*", "cat", "cat"), ("*", "dog", "cat")) 4 df1 = ("+", ("*", 2, "cat"), "dog") 5 df2 = ("+", ("*", 2, "cat"), ("*", "dog", "cat")) 7 assert test_derivative(f, df1, "cat") 8 assert not test_derivative(f, df2,"cat") 9 assert not test_derivative(f, dfi, "dog") 10 assert not test_derivative(f, dfi, 'donkey") 11 assert test_derivative(f, o, "donkey") 12 1 ### Hidden tests for test_derivative, 6 points. 1 ### Exercise: Implement apply distributive 2 3 def apply_distributive(e): ""Applies the distributive property to an expression e. 5 ### YOUR CODE HERE 4 *** 6 ] 1 ### Simple test for distributivity. 2 points. 2 3 ## Here is a definition of equality that disregards order. 4 def is_distributed (exp): 5 def is_plusminus(exp) : return isinstance(exp, tuple) and exp[@] in '+- if isinstance(exp, tuple): 9 op, ei, e2 = exp if op == and (is_plusminus (el) or is_plusminus (e2)): return false return is distributed (el) and is_distributed (22) 13 14 import random Boomvon 16 def value_equality(e1, e2): 17 return True 18 19 20 def applied distributivity(f, g): 21 return is_distributed(g) and value_equality(f, g) 23 # Simple test 24 ('*', ('+', 1, 2), ('-', 3, 4)) 26 f = ('+', ('-', ('*', 1, 3), ('*', 1, 4)), ('-', ('*', 2, 3), (**', 2, 4))) 27 applied_distributivity(apply_distributive(e), f) 25 e = 28 29 1 ### More complicated tests for distributivity. 2 points. 2 3 # More complex tests 4 5e = ("*', ('+', 1, 2), ('-', 3, 4)) 6 e2 = ('*', e, ('+', 5, 6)) 7 f = ('+', 8 (-', ('+', ('*', ('*', 1, 3), 5), ('*', ('*', 1, 3), 6)), 10 ('+', ('*', ('*', 1, 4), 5), ('*', ('', 1, 4), 6))), 11 (-', 12 ('+', ('*', ('*', 2, 3), 5), ('*', ('', 2, 3), 6)), 13 ('+', ('*', ('*', 2, 4), 5), ('*', ('*', 2, 4), 6)))) 14 15 applied_distributivity(apply_distributive (e2), f) 17 e = ('*', ('*', ('+', 1, 2), ('-', 3, 4)), (''', ('-', 5, 6), ('+', 7, 8))) 18 f = ('+', 19 (-", ('+', ('*', ('*', 1, 3), ('*', 5, 7)), ('*', ('*', 1, 3), ('*', 5, 8))), ('+', ('*', ('*', 1, 3), ('*', 6, 7)), ('*', ('*', 1, 3), ('*', 6, 8)))), 23 24 ('+', ('*', ('*', 1, 4), ('*', 5, 7)), ('*', ('', 1, 4), (':', 5, 8))), 25 ('+', ('*', ('*', 1, 4), (*, 6, 7)), ('*, ('*', 1, 4), ('*', 6, 8))))), 26 ('-', 27 28 ('+', (**, ('*', 2, 3), ('*', 5, 7)), ('*', ('*', 2, 3), ('*', 5, 8))), 29 ('+', ('*', ('*', 2, 3), ('*', 6, ?)), ('*', ('*', 2, 3), (**, 6, 8)))), 30 31 ('+', ('*', ('*', 2, 4), ('*', 5, 7)), ('*', ('*', 2, 4), ('*', 5, 8))), 32 ('+', ('*', ('*', 2, 4), ('*', 6, 7)), ('*', ('*', 2, 4), ('*', 6, 8)))))) 33 34 applied_distributivity(apply distributive(e), f) 35 36 4 1 ### Derivation of a leaf expression 2. 3 def derivate_leaf(e, x): ***"This function takes as input an expression e and a variable x, 5 and returns the symbolic derivative of e wrt. X, as an expression." 6 ### YOUR CODE HERE 7 1 ## Derivative of a leaf expression. 2 points. 2. == 1 3 assert derivate_leaf("x", "x") 4 assert derivate_leaf("x", "y") 5 assert derivate_leaf ("y", "z" 6 assert derivate_leaf(4, "x") @ 7. 1 ## Hidden tests for derivative of a leaf expression. 3 points. 2 1 ### Implement "derivate 2. 3 def derivate(e, x): ** "Returns the derivative of e wrt x. 5 It can be done in less than 15 lines of code. 6 ### YOUR CODE HERE EFE 7 1 ### Tests for derivate for single-operator expressions. 4 points. 3 assert derivate(('+', 'x', 'x'), 'x') == ('+', 1, 1) 4 assert derivate(('-', 4, 'x'), 'x') == ('-', 0, 1) 5 assert derivate(('*', 2, 'x'), 'x') ('+', ('*', 0, 'x'), ('*', 2, 1)) 6 assert derivate(('/', 2, 'x'), 'x') == ('7', ('-', ('*', 0, 'x'), ('*', 2, 1)), ('*', 'x', 'x')) 1 ### Hidden tests for 'derivate for single-operator expressions. 6 points. [] 1 ### Tests for derivate for composite expressions. 3 points. 2 3 e1 = ('*', 'x', 'x') 4 e2 = ('*', 3, 'x') 5 num = ('-', ei, e2) 6 e3 = (*', 'a', 'x') 7 den = ('+', el, e3) 8 e = ('7', num, den) 9 10 f = ('7', 11 ('-', 12 13 14 15 16 ('+', ('*', 1, 'x'), ('*', 'x', 1)), ('+', ('*', 0, 'x'), ('*', 3, 1))), ('+', ("*', 'x', 'x'), ('*', 'a', 'x'))), 18 ('-', ('*', 'x', 'x'), ('*', 3, 'x')), 19 28 ('+', ('*', 1, 'x'), ('*', 'x', 1)), ('+', ('*', 0, 'x'), ('*', 'a', 1))))), 22 ('*', 23 ('+', ('*', 'x', 'x'), ('*', 'a', 'x')), 24 ('+', ("*', 'x', 'x'), ('*', 'a', 'x')))) 25 26 assert derivate(e, 'x') == f [ ] 1 ### Hidden tests for "derivate for composite expressions. 7 points. 2 1 ### Implementation of test_derivative 2 2 3 def test_derivative(f, df, x, delta=0.8ee1, epsilon=0.1, num_tests=1808): See above." 5. ### YOUR CODE HERE 4. 1 ### Tests for test_derivative, 4 points. 2 3 f = ("+", ("*", "cat", "cat"), ("*", "dog", "cat")) 4 df1 = ("+", ("*", 2, "cat"), "dog") 5 df2 = ("+", ("*", 2, "cat"), ("*", "dog", "cat")) 7 assert test_derivative(f, df1, "cat") 8 assert not test_derivative(f, df2,"cat") 9 assert not test_derivative(f, dfi, "dog") 10 assert not test_derivative(f, dfi, 'donkey") 11 assert test_derivative(f, o, "donkey") 12 1 ### Hidden tests for test_derivative, 6 points. 1 ### Exercise: Implement apply distributive 2 3 def apply_distributive(e): ""Applies the distributive property to an expression e. 5 ### YOUR CODE HERE 4 *** 6 ] 1 ### Simple test for distributivity. 2 points. 2 3 ## Here is a definition of equality that disregards order. 4 def is_distributed (exp): 5 def is_plusminus(exp) : return isinstance(exp, tuple) and exp[@] in '+- if isinstance(exp, tuple): 9 op, ei, e2 = exp if op == and (is_plusminus (el) or is_plusminus (e2)): return false return is distributed (el) and is_distributed (22) 13 14 import random Boomvon 16 def value_equality(e1, e2): 17 return True 18 19 20 def applied distributivity(f, g): 21 return is_distributed(g) and value_equality(f, g) 23 # Simple test 24 ('*', ('+', 1, 2), ('-', 3, 4)) 26 f = ('+', ('-', ('*', 1, 3), ('*', 1, 4)), ('-', ('*', 2, 3), (**', 2, 4))) 27 applied_distributivity(apply_distributive(e), f) 25 e = 28 29 1 ### More complicated tests for distributivity. 2 points. 2 3 # More complex tests 4 5e = ("*', ('+', 1, 2), ('-', 3, 4)) 6 e2 = ('*', e, ('+', 5, 6)) 7 f = ('+', 8 (-', ('+', ('*', ('*', 1, 3), 5), ('*', ('*', 1, 3), 6)), 10 ('+', ('*', ('*', 1, 4), 5), ('*', ('', 1, 4), 6))), 11 (-', 12 ('+', ('*', ('*', 2, 3), 5), ('*', ('', 2, 3), 6)), 13 ('+', ('*', ('*', 2, 4), 5), ('*', ('*', 2, 4), 6)))) 14 15 applied_distributivity(apply_distributive (e2), f) 17 e = ('*', ('*', ('+', 1, 2), ('-', 3, 4)), (''', ('-', 5, 6), ('+', 7, 8))) 18 f = ('+', 19 (-", ('+', ('*', ('*', 1, 3), ('*', 5, 7)), ('*', ('*', 1, 3), ('*', 5, 8))), ('+', ('*', ('*', 1, 3), ('*', 6, 7)), ('*', ('*', 1, 3), ('*', 6, 8)))), 23 24 ('+', ('*', ('*', 1, 4), ('*', 5, 7)), ('*', ('', 1, 4), (':', 5, 8))), 25 ('+', ('*', ('*', 1, 4), (*, 6, 7)), ('*, ('*', 1, 4), ('*', 6, 8))))), 26 ('-', 27 28 ('+', (**, ('*', 2, 3), ('*', 5, 7)), ('*', ('*', 2, 3), ('*', 5, 8))), 29 ('+', ('*', ('*', 2, 3), ('*', 6, ?)), ('*', ('*', 2, 3), (**, 6, 8)))), 30 31 ('+', ('*', ('*', 2, 4), ('*', 5, 7)), ('*', ('*', 2, 4), ('*', 5, 8))), 32 ('+', ('*', ('*', 2, 4), ('*', 6, 7)), ('*', ('*', 2, 4), ('*', 6, 8)))))) 33 34 applied_distributivity(apply distributive(e), f) 35 36
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


