so for this lab I was able to create the matlab code for question #1 and #2 which are for #1

clear all

clc

L= input('what is the length of the bar');

N= input('what is the number of intervals ');

q0= input('what is this value');

E= 2.1e11;

A= 0.02;

h = L/N;

k= 1000000;

A_1= zeros(N);

for c=2:N-1

A_1(c,c)=-2;

A_1(c,c-1)=1;

A_1(c,c+1)=1;

end

A_1(N,N-1)=2;

A_1(1,1)=-2;

A_1 (1,2)= 1;

A_1(N,N)=-2-2*h*k/(A*E);

A_1;

x= h:h:L;

for i= 1:N

if x(i)

q(i)= q0*((2*x(i))^2)/L^2;

else

q(i)=q0*(2-2*x(i)/L);

end

end

A_1

q

b= zeros(N,1);

for i= 1:N

b(i)= - ((h^2)*q(i)/(E*A));

end

b

U= A_1^-1*b

For problem #2 the code is

clc

clear all

E= 2.1e11;

A= 0.02;

L= 5;

q0= 5000;

G = [2 4 8 16 4096]

for j= 1:5

N= G(j);

k= 1000000;

A_1= zeros(N);

h = L/N;

for c=2:N-1

A_1(c,c)=-2;

A_1(c,c-1)=1;

A_1(c,c+1)=1;

end

A_1(N,N-1)=2;

A_1(1,1)=-2;

A_1 (1,2)= 1;

A_1(N,N)=-2-2*h*k/(A*E);

A_1

x= h:h:L;

for i= 1:N

if x(i)

q(i)= q0*(2*x(i))^2/L^2;

else

q(i)=q0*(2-2*x(i)/L);

end

end

A_1

q

b= zeros(N,1);

for i= 1:N

b(i)= - ((h^2)*q(i)/(E*A));

end

b

U= A_1\b

plot (x,U)

hold on

end

So now I need help problem #3 and #4 the problem is continuous so you will have to use my code 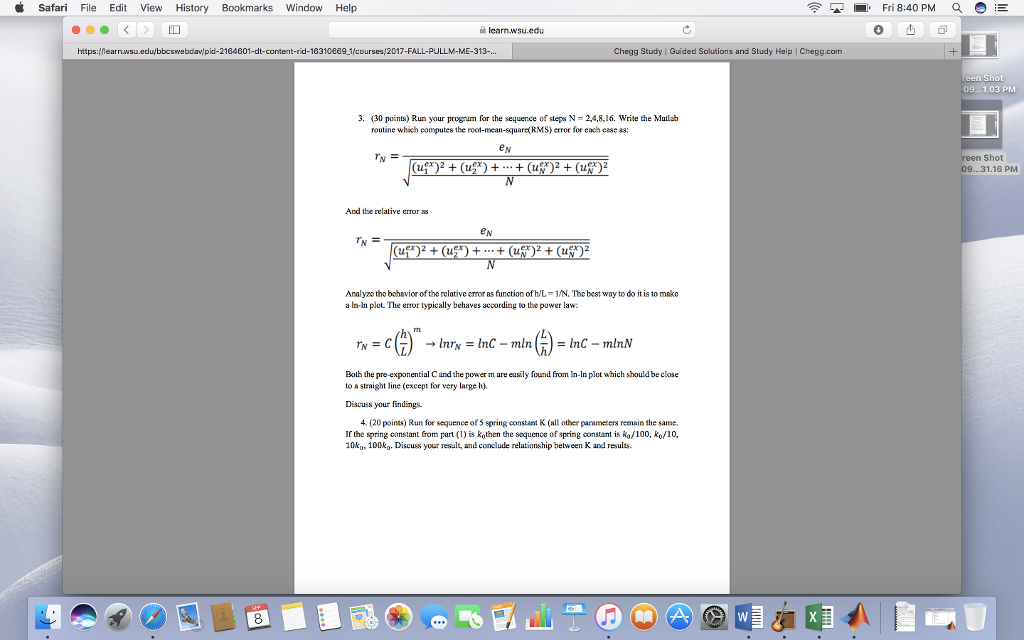. I really need help on this one it is in Matlab this is the whole lab using my code #3 and #4 question is better understood with the whole lab together.

i Safari File Edit View History Bookmarks Window Help 11 Fri 8:40 PM 16310869 1/courses/2017-FALL-PULLM-ME-313-... Chegg Study Guided Solutions and Study Help | Chegg.com 09...1.03 PM 3. (30 points) Run your program for the sequence of steps N-2,4,8,16. Write the Matlab routine which computes the root-mean-square RMS)eor for each case as: reen Shot 09...31.16 PM And the relative error as eN Analyze the bohavior of the relative crror as function ofh/L- IN. The best wny to do it is to make a ln-In ploL The er typically behaves acording to the power law Both the pre-exponential C and the power m are eusily found from Im-In plot which should be close to a straight line (except for very large h) Discuss your findings. 4. (20 points) Run foe sequence of S spring constant K (al other parameters remain the same. If the spring constant from part (1) is kothen the sequence of spring constant is ko/100, ko/10, 10k, 100ko. Discuss your result, and conclude relationship between K and results