Use python:

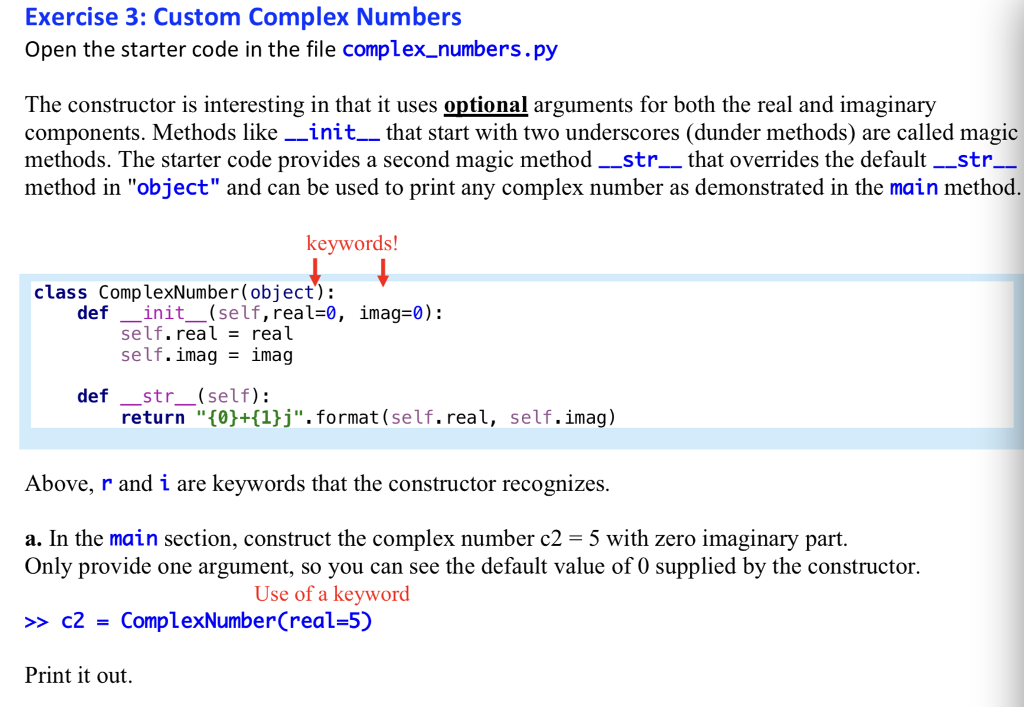
class ComplexNumber(object): def __init__(self,real=0, imag=0): self.real = real self.imag = imag def __str__(self): return "{0}+{1}j".format(self.real, self.imag) # complete this stub method for __add__()  def __add__(self, other): real = 0 # fix this stub  imag = 0 # fix this stub  return ComplexNumber(real, imag) # complete this stub method for add()  def __mul__(self, other): return ComplexNumber(0, 0) # fix this stub  if __name__ == "__main__": # 1. Create a new ComplexNumber object  c1 = ComplexNumber(3,4) # Print out the first complex number c1. Note this automatically calls the __str__ magic method.  print("Complex number c1 = ", c1) # 2. Create another ComplexNumber object equal to 5. Provide only one argument!  c2 = ComplexNumber(real=5) # Print out the second complex number c2.  print("Complex number c2 = ", c2) # 3. Create another ComplexNumber object equal to 6i. Provide only one argument!  # add code here   # Print out the third complex number c3.  # add code here   print(" Complex Arithmetic") # 4. Add c1 and c2 using the + operator defined by the magic method __add__  print("The sum of c1 and c2 is:", c1 + c2) # 5. Multiply c1 and c2 using the * operator defined by the magic method __mul__  # add code here. 

Exercise 3: Custom Complex Numbers Open the starter code in the file complex_numbers.py The constructor is interesting in that it uses optional arguments for both the real and imaginary components. Methods likeinit that start with two underscores (dunder methods) are called magic methods. The starter code provides a second magic method-str that overrides the defaultstr method in "object" and can be used to print any complex number as demonstrated in the main method. keywords! class ComplexNumber(object): -init(self, real-0, self. real- real self.imag-imag def imag=0): def str_(self): return "(01+{1}j". format (self. real, self.imag) Above, r and i are keywords that the constructor recognizes a. In the main section, construct the complex number c2-5 with zero imaginary part. Only provide one argument, so you can see the default value of 0 supplied by the constructor. c2 = ComplexNumber(real-5) Print it out. Use of a keyword