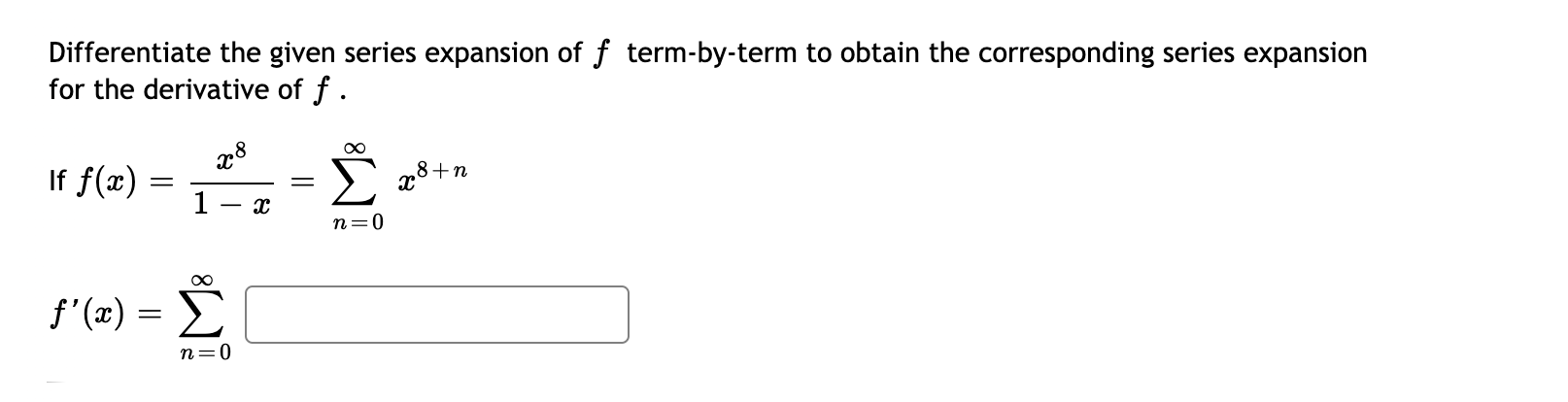
Use term-by-term differentiation or integration to find a power series centered at x = 0 for: f(x) = tan -1 (x3) = n=0Find the radius of convergence for: 3n n=1\fGiven that as\" with convergence in (-1, 1), find the power series for with center 0 1+3m9 1 1 13:: H: Identify its interval of convergence. The series is convergent from a: = C] , left and included (enter Y or N): C] to a: = C] , right end included (enter Y or N): C] Differentiate the given series expansion of f term-by-term to obtain the corresponding series expansion for the derivative of f . um): 15: = :0: 938+" n=0 W) = i n=0 Integrate the given series expansion of f term-by-term from zero to a: to obtain the corresponding series expansion for the indefinite integral of f. 3m2 _1 If f(:c) (1 + 9:3)2 =0( 1)\" 341333\