Question: Access the Sampling Distribution of the Sample Proportion web app. a. For p = 0.5 and a sample of size n = 3, the graph

Access the Sampling Distribution of the Sample Proportion web app.
a. For p = 0.5 and a sample of size n = 3, the graph of the sampling distribution is given below. (This is the graph corresponding to the table in Exercise 7.49, part b.) Compute the mean of the sampling distribution from first principles, i.e., using the formula gxP1X = x2. The standard deviation of the sampling distribution is equal to 0.289.
b. Now, using the app, simulate the sampling distribution for a population proportion when p = 0.5 and n = 3, using 10,000 simulations. Do the graph and the results from the simulations agree? Compare the shapes, means, and standard deviations from the two graphs. (The mean and standard deviation of the 10,000 generated sample proportions are displayed in the title of the graph for the sampling distribution in the app.)

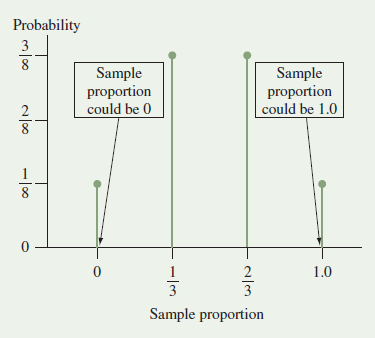
Probability 3 Sample proportion could be 0 Sample proportion could be 1.0 1.0 Sample proportion 2/3 -l3 -l00

Step by Step Solution

★★★★★

3.37 Rating (172 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a The mean of the sampling distribution is 018 13... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Document Format (2 attachments)

1544_605d88e208e01_676264.pdf

180 KBs PDF File

1544_605d88e208e01_676264.docx

120 KBs Word File

Students Have Also Explored These Related Statistics The Art and Science Questions!

Access the Sampling Distribution of the Sample Proportion web app. When p = 0.6 and the sample size n = 3, the mean and standard deviation of the sampling distribution (given in the table in part a...

a. For the population, find the proportion of odd numbers. b. Table describes the sampling distribution of the sample mean. Construct a similar table representing the sampling distribution of the...

Because they enable efficient procedures for evaluating answers, multiple-choice questions are commonly used on standardized tests, such as the SAT or ACT. Such questions typically have five choices,...

8.62 Bootstrap interval for the proportion We want a 90% confidence interval for the population proportion of students in a high school in Dallas, Texas, who can correctly find Iraq on an unlabeled...

7.52 Simulating pizza preference with p 0.5 Access the Sampling Distribution of the Sample Proportion web app. a. For p = 0.5 and a sample of size n = 3, the graph of the sampling distribution is...

The following table shows the result of the 2018 General Elections in Pakistan, along with the vote share predicted by several organizations in the days before the elections. The sample sizes were...

1.25 Simulate with the Sampling Distribution for the Sample Proportion web app Refer to Activity 2 on page 47. a. Repeat the activity using a population proportion of 0.60: Take at least five samples...

Question 8, 1.2.18-App HW Score: 66.18%, 15.22 of 23 points Points: 0 of 1 Save Suppose Ebola virus disease outbreaks have a case fatality rate of 80% (meaning 80% of people who get it die). In a...

1.26 Margin of error Refer to the Sampling Distribution of the Sample Proportion web app used in Activity 2. a. For a population proportion of 0.50, simulate a random sample of size 1000. What is the...

7.45 CLT for custom population Access the Sampling Distribution for a Sample Mean web app and select Build Own as the shape for the population distribution. By typing numbers into the text field, you...

A timber [E = 12 GPa] beam is loaded and supported as shown in the following figure The cross section of the timber beam is 100 mm wide and 300 mm deep. The beam is supported at B by a 12-mm-diameter...

The density of atmospheric air is about 1.15 kg/m3, which we assume is constant. How large an absolute pressure will a pilot see when flying 1500 m above ground level where the pressure is 101 kPa.

A firm could offer a pricing decision such as marking all cold and cough medications 1 0 % off right before or at the beginning of cold / flu season. This could cause consumers to stock up before...

The prisoners dilemma is a two-person game illustrating that a. the cooperative outcome could be worse for both people than the Nash equilibrium. b. even if the cooperative outcome is better than the...

5.3 Counselor availability You visit your counselors office at 10 randomly chosen times, and he is not available at any of those times. Does this mean that the probability of your counselor being...

5.4 Airline accident deaths Airplane safety has been improving over the years. From 2000 to 2010, the average number of global airline deaths per year was over 1000, even when excluding the nearly...

6.91 Multiple choice: Guess answers A question has four possible answers, only one of which is correct. You randomly guess the correct response. With 20 such questions, the distribution of the number...

18. The most commonly used form required by TRID at settlement is: A. the seller's property disclosure. B. the lead-based paint disclosure. C. the closing disclosure (CD). D. the loan estimate (LE)

Rachel is 40 years old. She plans on retiring in 25 years when she will be 65 years old. Rachel believes she will live until she is 95. In order to live comfortably, she needs a substantial...

Homework - Chapter 13 Seved Help Save & Exit Submit Check my work 3 You have been given the following return information for a mutual fund, the market index, and the risk free rate. You also know...