Make the given changes in Example 1 of this section and then solve the resulting system of equations.

In the second equation, change the constant to the right of the = sign from 11 to 12, and in the third equation, change the constant to the right of the = sign from −4 to −14.

Data from Example 1

Solve the following system of equations:

Thus, the solution is x = 1/2 y = −3, z =2/3 Substituting in the equations, we have

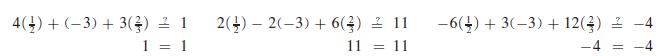
(1) (2) (3) (4) (5) (6) (7) (8) 4x + y + 3z = 1 2x - 2y + 6z = 11 -6x + 3y + 12z = -4 8x + 2y + 6z = 2 2x -2y+ 6z 11 10x + 12z = 13 12x + 3y + 9z = 3 - 6x + 3y + 12z = -4 18x 3z = = 10x + 12z = 13 72x 12z 28 82x 41 18(+) = = (10) (11) (12) (13) (14) 4() + y + 3() = 1 (15) 2 + y + 2 = 1 (16) y = -3 x = 4 3z = 7 - 3z: = -2 z = 3/ (1) multiplied by 2 (2) adding (1) multiplied by 3 (3) subtracting (5) (7) multiplied by 4 adding substituting (10) in (7) substituting (13) and (10) in (1)