![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()



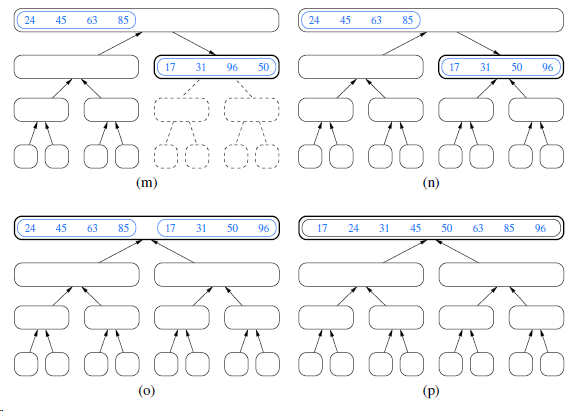
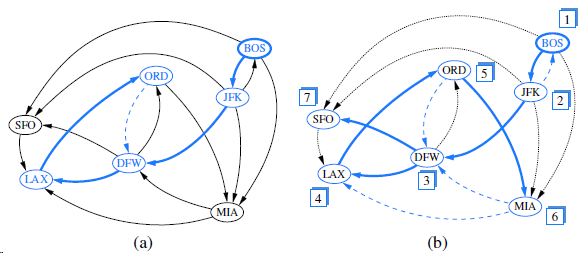
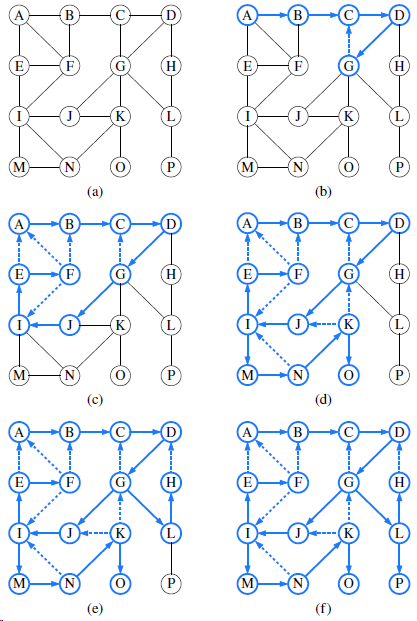
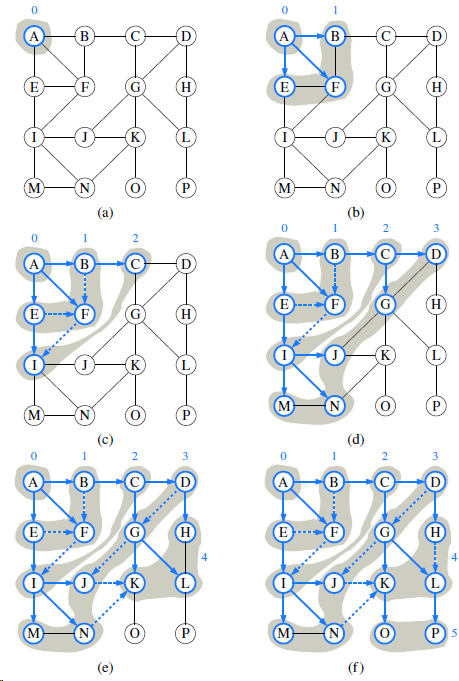
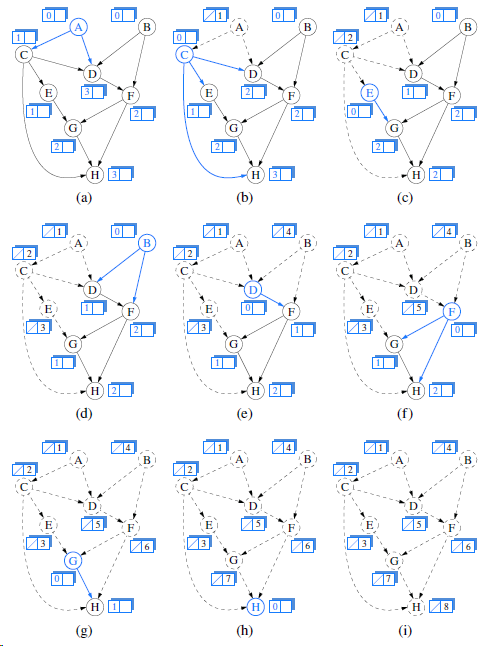
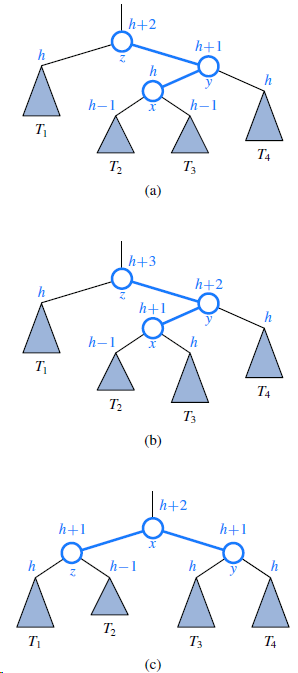

![/** Sort the subarray S[a.b] inclusive. */ private static <K style=](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1544/6/2/5/3785c111ce2684f01544607938880.jpg)
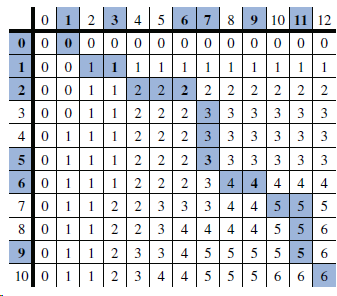
![1 private static int[] computeFailKMP(char[ ] pattern) { int m = pattern.length; int[ ] fail = new int[m]; int j = 1; 2](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1544/6/2/8/3255c112865dcea01544610886310.jpg)