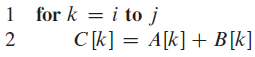![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()



![1 for i = 1 to n determine j such that i e K; if j + m + 1 extracted[j] = i let I be the smallest value greater than j f](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/3/0/8/6555c1b89ef5976b1545291196083.jpg)
![if Sij = Ø , max {c[i,k]+ c[k, j]+ 1} _if Sij + Ø . c[i, j]= ak ES¡J](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/1/5/2/5175c192805728f01545135083612.jpg)
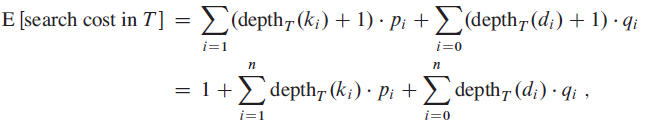
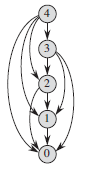
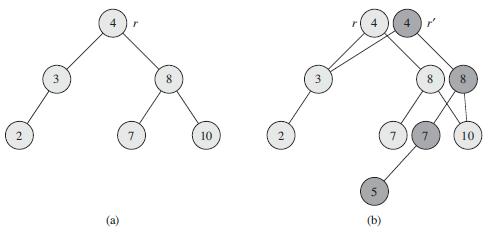
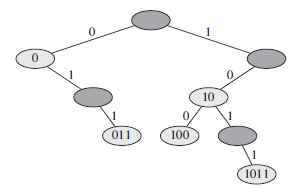
![j – k – 1 j - k +1 ΣΣ Σ k k – i – 1 E[X&] < 2(EE: j - i +1 i=1 j=k k – i +1 i=1 j=k+1](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1544/7/9/2/3415c13a915650691544720329842.jpg)
![0 if A[i] < A[p] , 1 if A[i] style=](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1544/7/2/0/7445c129168decb81544703257455.jpg)

![1 parallel for i = 1 to A.length C[i] = A[i] + B[i]](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/6/4/8/9235c20bb1b9f64c1545491186166.jpg)
![1 n = A.length 2 grain-size = ? = [n/grain-size] 4 for k = 0 to r – 1 spawn ADD-SUBARRAY(A, B, C,k · grain-size + 1,](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/6/4/8/9235c20bb1ba71c01545491186222.jpg)