![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


![g[nw[n] 3 v[n] x[n] y[n] 1.3 1.8 0.3 4.5 -0.8 0.4 2.](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/9/2/2/6335c24e8490acc91545905216057.jpg)
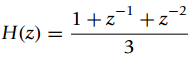
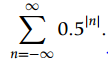
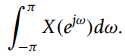
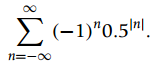
![п -Ө) u[n], х-\n] — u[—п — 1] х[n] 3](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/8/3/1/6125c2384bcd136e1545814197590.jpg)
![3+n -2 <n< -1 t[n] = {3 – n 0<n<2 otherwise](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/8/3/1/8535c2385ad655cc1545814438071.jpg)
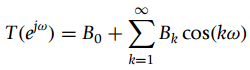
![1 -1/2 < w <1/2 0 otherwise in (–x,7] H(](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/8/3/1/9565c23861449cb51545814541070.jpg)
![x1[n] = 1+ style=](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/8/3/2/1095c2386ad7c10f1545814694238.jpg)
![1 -0.47 < w < 0.4M 0 otherwise in (–x,7] H(e](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/8/3/2/4395c2387f7511971545815023855.jpg)
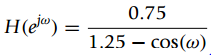

![x[n/2] n even x2[n] = otherwise](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/8/3/2/8405c238988012291545815424676.jpg)
![sin(л(n — 10)/3) п (п — 10) -,п # 10, h[10] — 1/3. h[n]](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/8/3/2/9385c2389eaf02a11545815523712.jpg)
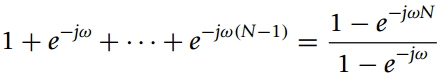
![1 п%3D 0, 1, 2 x[n] = 0o therwise](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/8/4/5/5815c23bb4dee81a1545828165839.jpg)
![-2 <n< 2 h[n] otherwise](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/9/0/2/1535c249849b0c921545884736758.jpg)
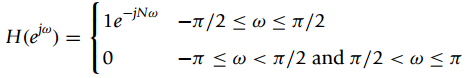
![N-1 0 <n< N – 1 (1) x[n] = Xe2a nk/N k=0 N-1 style=](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/9/0/5/2815c24a481457641545887864699.jpg)
![N-1 | in]-Σχ,ελπn:/N Хь 0 <n< N – 1 k=0](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/9/0/5/6025c24a5c2698f81545888185569.jpg)
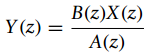
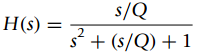
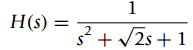
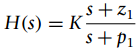
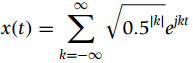
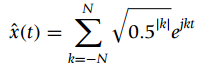
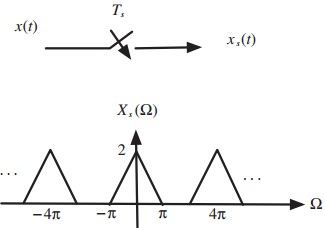
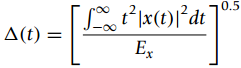
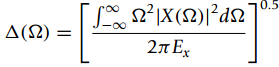
![n = -1,0, 1 x[n] = {0.5 n = 2 otherwise](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/4/9/3/2455c1e5afd832561545475821399.jpg)
![x[n] y[n] (X) cos(n/ 4)](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/4/9/3/7925c1e5d20dacc21545476368829.jpg)
![n+4 γin] Σt x[k] k=n-2](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/4/9/4/1565c1e5e8cc8d7d1545476732768.jpg)
![п x[n] п x[п] 0 1.0 3 0.7 1 1.2 4 1.2 2 0.9 5 1.0](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/4/9/4/4145c1e5f8e676a11545476990232.jpg)
![y[n] = x[n] + x[n – 1] +x[n – 2]](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/4/9/4/4145c1e5f8e78da31545476990326.jpg)
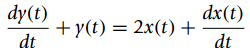
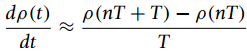
![2 e[n] yla) D. D Ma-1]](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1606/4/6/9/5455fc0c7a9848e71606469545412.jpg)