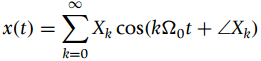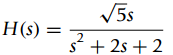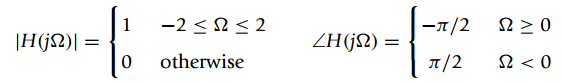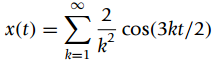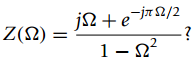![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


![ο0 γίn]Σο.5)' x[n -k k=0 'x[n – k] (0.5](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/6/4/2/4265c20a1ba5fad91545625014126.jpg)
![п I (п - k+ 2)x[k] УIn] %3D — k=-00](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/6/4/2/7835c20a31f1f15d1545625371164.jpg)
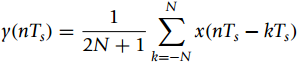
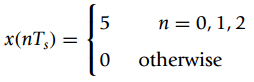
![n = 0, 3 hT[n] = %3D otherwise](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/6/4/3/0935c20a455019f01545625680717.jpg)
![0, 1, 2 п %3 x[n] otherwise](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/6/4/3/3105c20a52e051441545625898000.jpg)
![n = 0, 1, 2, 3, 4, 5 x[n] = otherwise](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/6/4/3/3105c20a52e20d791545625898155.jpg)
![N-1 N-1 x[n – k] Уx[п — k], (В) (A) y[n] = k=0 2 (B) y[n] = k=-N+1](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/6/4/4/2555c20a8df6bc801545626843580.jpg)
![Σ Κ |x[n] εχ n=-00 ||](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/6/4/4/9805c20abb45b5431545627568223.jpg)
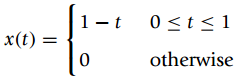
![3D x(п— 5k] У x[n — 5k] y[n]: k=-00](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/6/4/6/2125c20b084375ad1545628800302.jpg)
![[r(t) – r(t – 3)]-Ir(t – 20) – r(t – 30)] e(t) = 3 10](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/6/4/7/0885c20b3f0056021545629676161.jpg)
![γίn]Σw[n-k γ[n] kx[n k=0 k]](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/6/4/7/6455c20b61df2b031545630233349.jpg)
![-1 x[n] < 0 s[n] = sign(x[n]) = {0 x[n] = 0 x[n] style=](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/6/6/7/2805c2102d00c44f1545649867640.jpg)
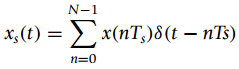
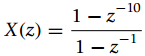
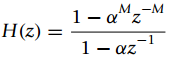
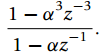
![e[n] r[n]- Delay y[n]](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/6/7/2/8845c2118b438aae1545655471408.jpg)
![n = 0, 3 n = 0, 1 Output y[n] n = 1, 2 Input x[n] = otherwise otherwise](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/6/7/3/0865c21197ed708f1545655673896.jpg)
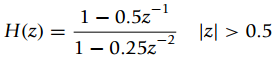
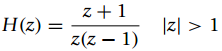
![n < 0 Input x[n] = (-1)](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/6/7/3/3205c211a6891d391545655907772.jpg)
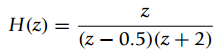
![п %3D 0, 1 п hin] 3D { 0.25 п%3D2 = 2 otherwise](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/8/1/7/3535c234d098cef01545799938707.jpg)
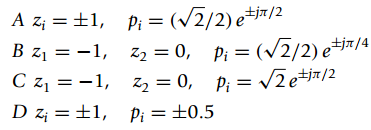
![|S(S)? |N()P f (KHz) 10 r[n] y/n] H(2) x(t) y(t) Sampler Ideal D/A f.](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/8/1/7/8815c234f19878d31545800466445.jpg)
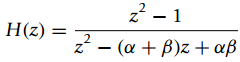
![Differentiator w[n] = x[n] – x[n – 1] w[n] У[n — 1] Smoother y[n] = 3 3 3.](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/8/1/8/1915c23504f7063c1545800776546.jpg)
![y[n] x[n] 0.5 0.25 ২](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/8/1/8/2785c2350a6aaf911545800863868.jpg)
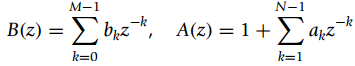
![d = [-} 1], d= A : b = 3 1/3 -1/3 1](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/8/1/8/6595c235223610211545801244167.jpg)
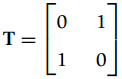
![г - (оь.] —ај -аз т 0 b2 b = A =](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/8/1/8/7635c23528b445541545801347393.jpg)
![—ај -аz т C = |b, b, b. A. b1 d = [1 0] -a, 1 A, b. b2 -аз 0](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/8/1/9/0425c2353a2954281545801627535.jpg)
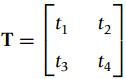
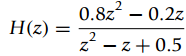
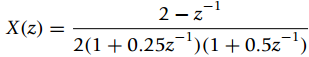
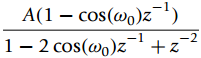
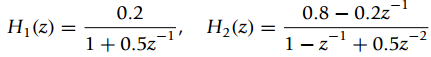
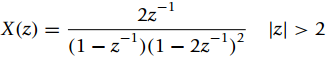
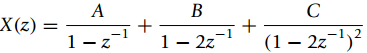
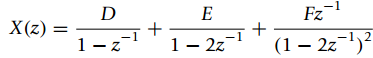
![=[1o] [0 1] = style=](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/4/0/1/9725c1cf674c60e21545384550332.jpg)
![BI ,d = [1 ] -11 ,bo A, -1 2 0 || ||](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/4/0/1/8995c1cf62be89dd1545384477349.jpg)
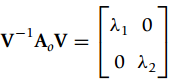
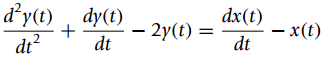
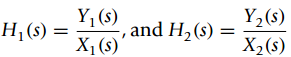
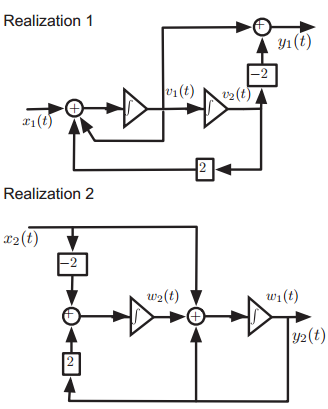
![.& - [, ъ] -a1 -ao Ac bị bo I|](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/3/9/6/4765c1ce0fc9bbdd1545379054355.jpg)
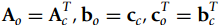
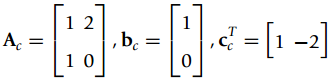
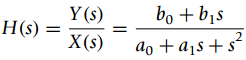
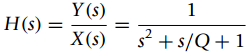
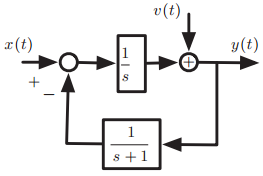
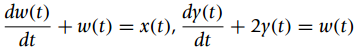
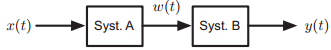
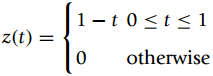
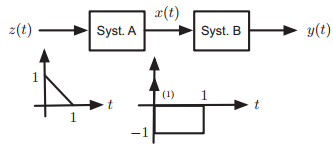
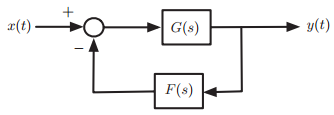
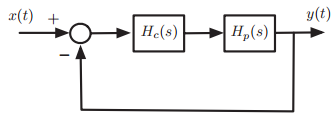
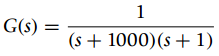
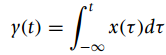
![-[u(t) — и(t — Тo)] To x(t) = ||](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/3/8/3/8985c1cafda0e5791545366476222.jpg)
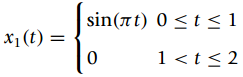
![dy(t) dt —D 0.5[x(t) — х(t — 2)]](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/3/2/8/2595c1bd683f34eb1545310839041.jpg)