![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


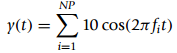
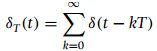
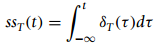
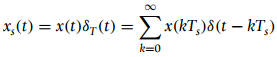
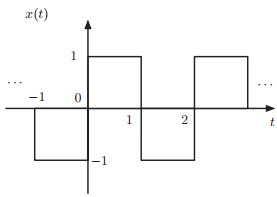
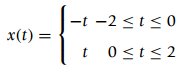
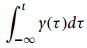
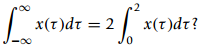
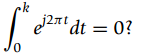
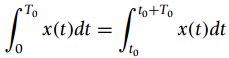
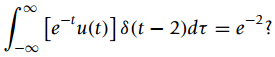
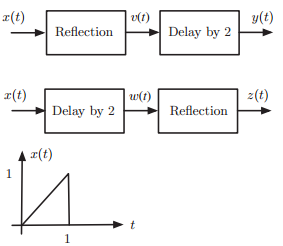
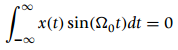
![[x(t) + x(-t)] sin(2,t)dt = 0 %3D](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1544/8/8/3/7585c150e2ee72f21544866335985.jpg)