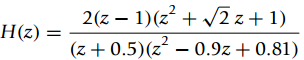![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


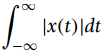
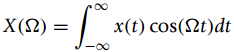
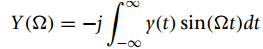
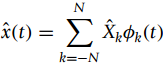
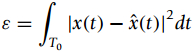
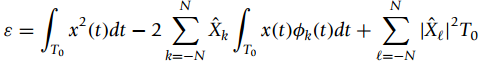
![-(m²+n²) e 4σ4 h[m, n] - 3σ< m< 3σ, -3σ<n< 3 σ](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1566/8/1/6/3385d63b8523a7391566799553534.jpg)
![N-1 — )2т km M-1 м- — )2тёn' E [m, n] exp ( en X (k, €) |exp Σ т-0 м п-0 X(т,0) - )2лkm I X(m, 0)ехp (](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1566/8/1/5/7215d63b5e9c1a0b1566798937142.jpg)
![1 0< m< (M1 – 1), 0<n< (N1 – 1) O M1 <m < (M – 1), N1 <n < (N – 1) r[m,n]](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1566/8/1/5/7435d63b5ffc13e51566798959131.jpg)


![h„[m, n] = ő[m, n] – 8[m – 2, n] + 26[m, n – 1] – 26[m – 2, n – 1] + ő[m, n – 2] – 6[m – 2, n –](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1566/5/7/8/9355d6018f7d674e1566562143765.jpg)
![Y1[m, n] = (h, * x)[m,n], y2[m, n] = (h, * 1)[m, n] y[m, n] = V(yn [m, n])? + (y2[m, n])²](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1566/5/7/8/9785d601922561a81566562186265.jpg)
![бт, п] + 25(m — 1, п] + 36|т — 2, п] + 46(m, п — 1] + 56(т - 1, п — 1] + 66|m - 2, п — 1] гm, п] +](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1566/5/7/8/3485d6016ac07f2e1566561555931.jpg)
![|h m, п] %3D бт, п] + бm — 1, п] — б[т, п — 1]— 6\т — 1, п — 1]](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1566/5/7/8/3705d6016c20aa4e1566561577906.jpg)
![r[m, n] = style=](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1566/5/7/6/7425d601066e3f8a1566559950856.jpg)
![r[m, n] = am+](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1566/5/7/6/6825d60102a8f79d1566559890528.jpg)
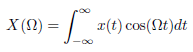
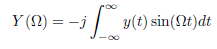
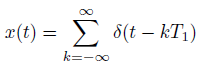
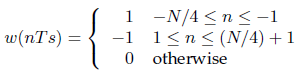
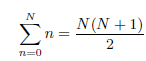
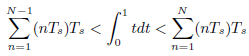
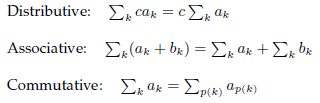
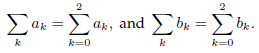
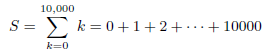
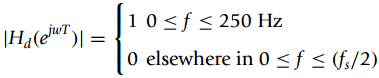
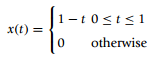
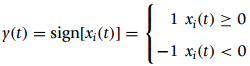
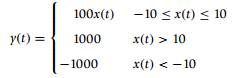
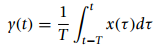

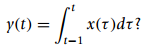
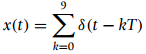
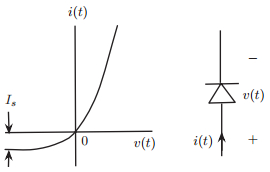
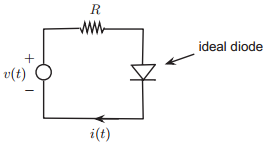
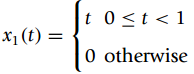
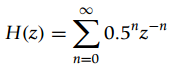
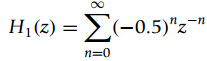
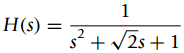
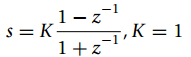
![N,N2 gcd[N1, N2]](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/6/4/6/7605c20b2a81de7c1545629348258.jpg)
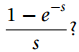
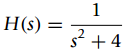
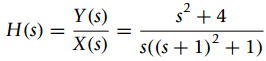
![y[n] = 1+(2/k) cos(0.2t kn) 0 < n < ∞. k=1 |](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/8/3/4/1685c238eb8cd4531545816753537.jpg)
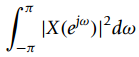
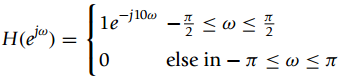
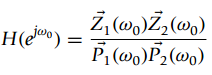
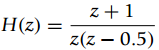
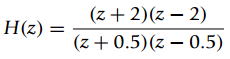
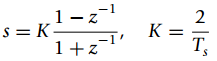
![y[n] r[n] + e[n]](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/9/2/2/4815c24e7b1242fd1545905064130.jpg)