A satellite control system is modeled as shown in Fig. P11.4-6. This system is described in Problem 1.4-1.
For this problem, ignore the sensor gain and let D(z) = 1. In addition, K = 1, T = 1 s, and J = 4. As stated in Problem 9.2-4, a state model for this system is given by

where x₁(k) is angular position and x₂(k) is angular velocity.

(a) Determine by hand the gains required to minimize the cost function

with N = 1. The value of N is chosen to be unity to limit the calculations.
(b) Use MATLAB to solve part (a) for N = 20. Sketch the calculated gains versus k.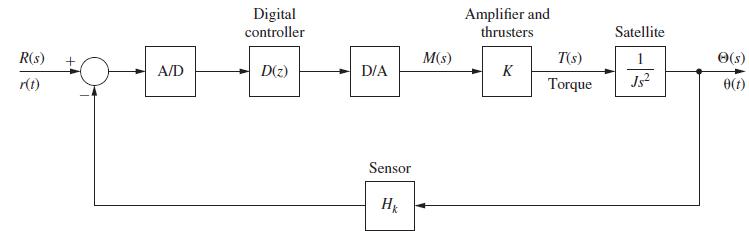

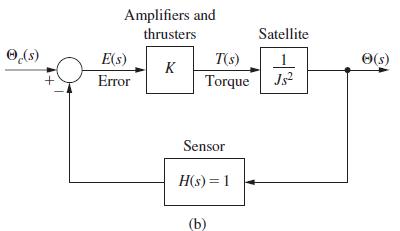
Problem 1.4-1

- [6 1] x(4) + [0.235 x(k+ 1) = y(k) [10]x(k) = u(k)