Consider the unit disk problem with displacement boundary conditions u r + iu = h() on C: = e i . Using Cauchy

Consider the unit disk problem with displacement boundary conditions u_r + iu_θ = h(ς) on C: ς = e^iθ. Using Cauchy integral methods described in Section 10.5, determine the form of the potentials γ (z) and Ψ(z).

Data from section 10.5

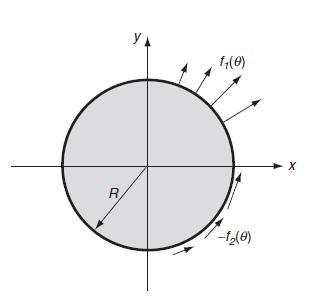
We now develop some solutions of particular plane elastic problems involving regions of a circular domain. The process starts by developing a general solution to a circular region with arbitrary edge loading, as shown in Fig. 10.8. The region 0