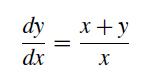![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


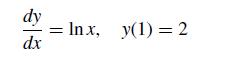


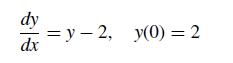


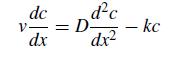
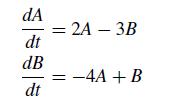

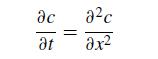
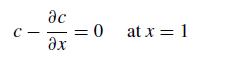
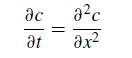
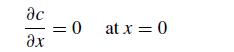
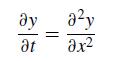
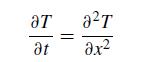
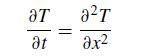

![5 --[:] b 10 0](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1697/6/1/3/888652f884047fab1697613886502.jpg)
![2 4 2 6 13 9 2 8 17 1 = [ 2 1 L = 00 1 ;] - [ 0 L3,2 1 2 62 1 4 003 0 X = X1 X2 X3](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1697/6/1/3/858652f88229a16d1697613856894.jpg)

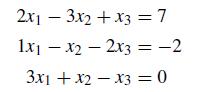

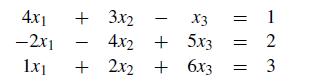
![[2][3]-[2] y 12](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1697/6/1/3/993652f88a915a411697613990938.jpg)
![6 [][][] y 15 Z 6 1 2 3 4 5 6 1 3 2](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1697/6/1/4/011652f88bb51a001697614009163.jpg)
![A = [2, 4] -1](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1697/6/1/4/075652f88fb3b2d91697614072841.jpg)
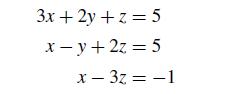
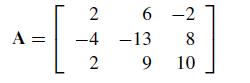
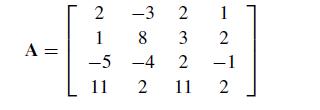
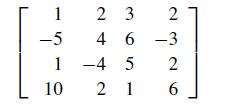
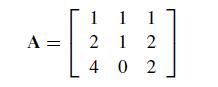
![A = [ 1 ] 12 01](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1697/6/1/4/190652f896e9709f1697614189158.jpg)
![3 - [22] 1 A =](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1697/6/1/4/210652f898269d691697614208016.jpg)
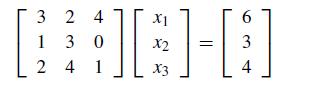

![1 A=[27] 1](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1697/6/1/5/139652f8d23d35c61697615137581.jpg)


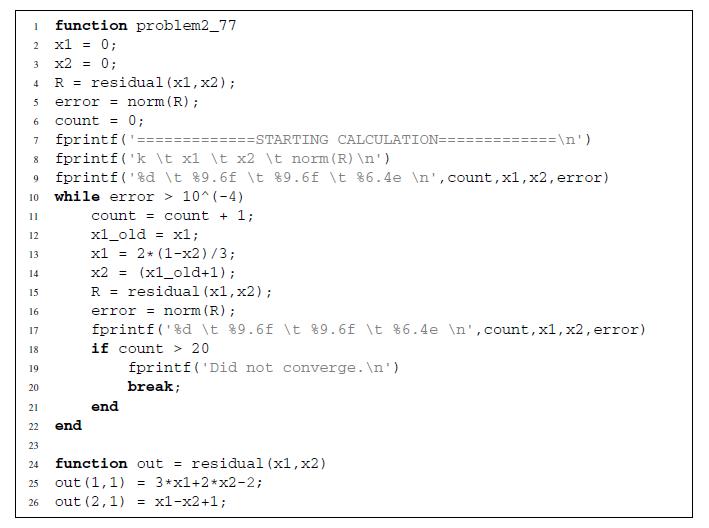
![1 function problem2_76 2 A = [2,3,1;-2, 3,2; 1, 2,5]; 3 b = [1; 4; 2]; 4 x = [0; 0;0]; 5 6 7 8 9 10 12 13 15](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1697/6/1/5/211652f8d6bcdc6c1697615208851.jpg)
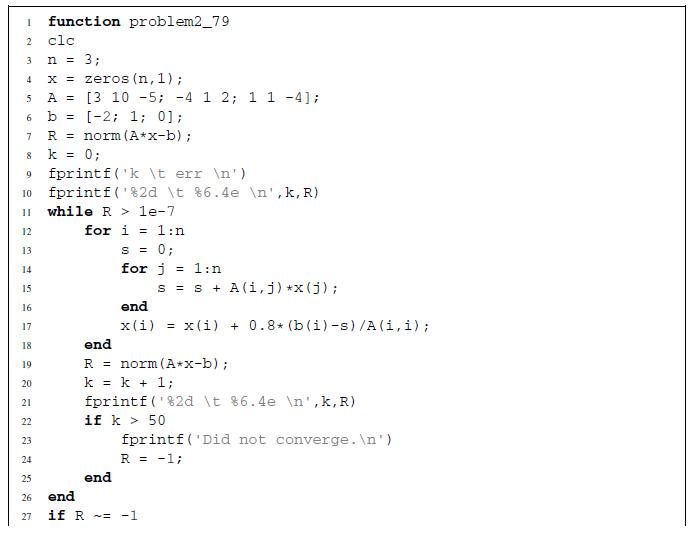

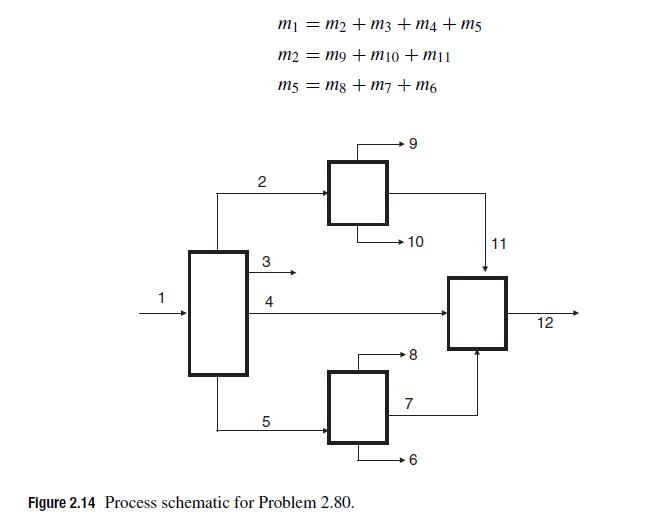

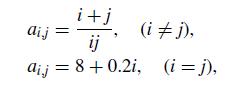
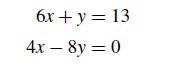
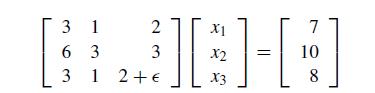
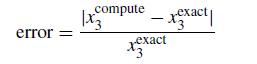


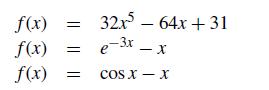
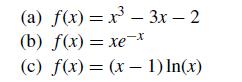
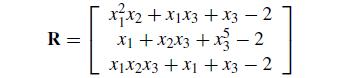
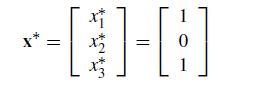
![[:] x(0) = x* +](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1697/6/2/5/075652fb3f3380e31697625073435.jpg)

![1 - 1 Z + sin(y) = 0 x-os(z) - z=0 X + os[(x-z)] - 2e = 0 Z](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1697/6/2/5/225652fb489531491697625222486.jpg)