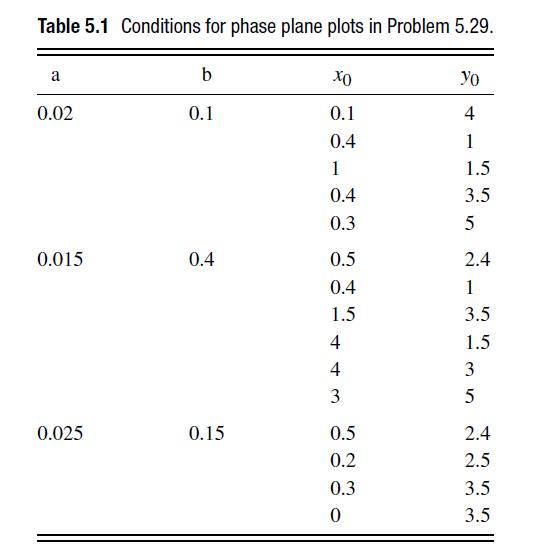
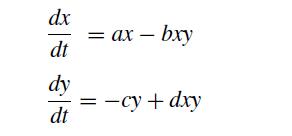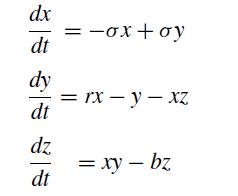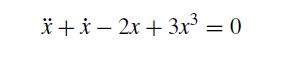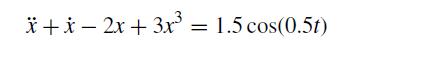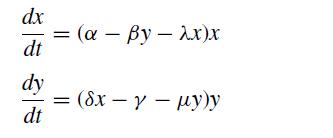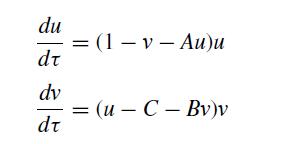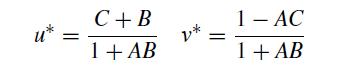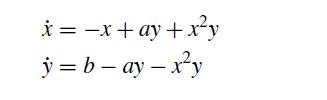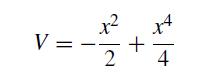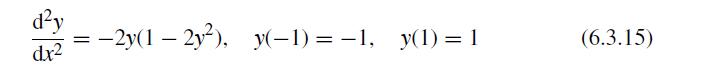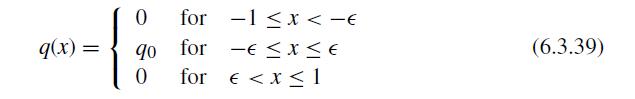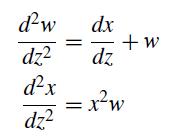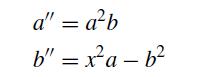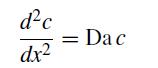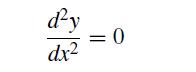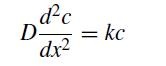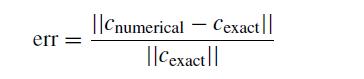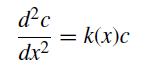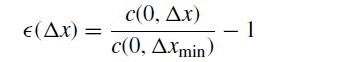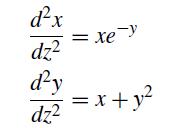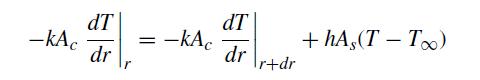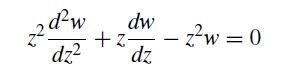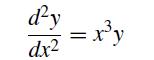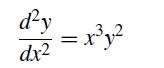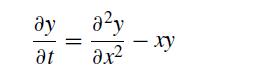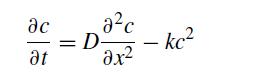![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()




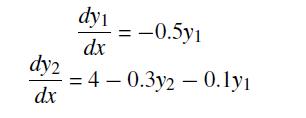
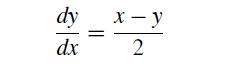
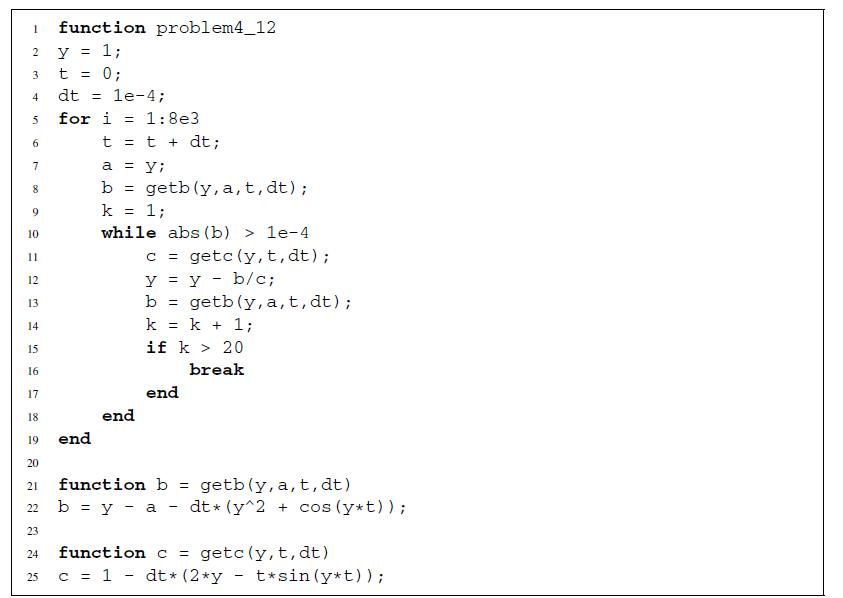
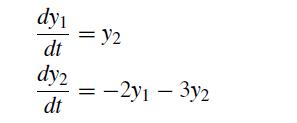

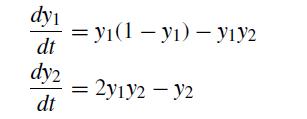
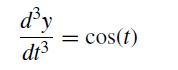
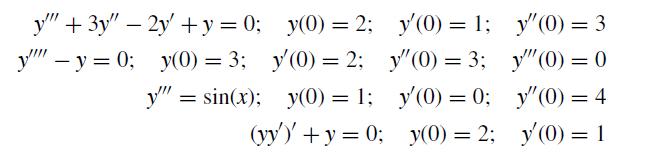
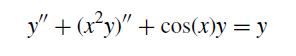


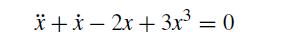
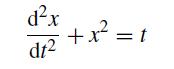
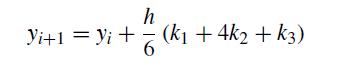
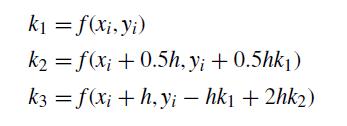
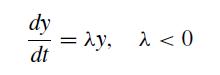
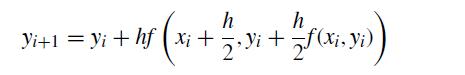
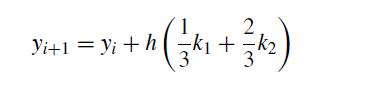
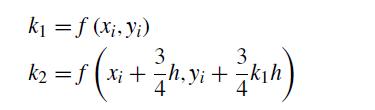
![h Yi+1=Yi+[f (vi) + f (Vi+1)]](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1697/6/8/8/2266530aaa23f7fe1697688223088.jpg)

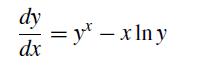
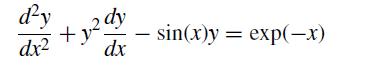
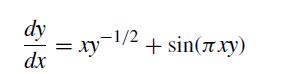
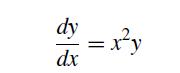
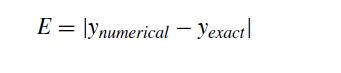
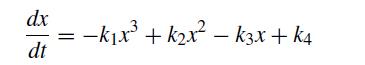
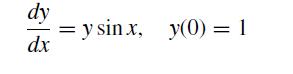
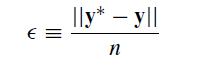
![dy = dx = sin(x) cos(y) exp(-[x + y)]](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1697/6/8/9/4906530af928f39b1697689488240.jpg)
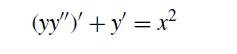
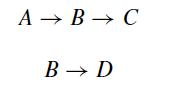
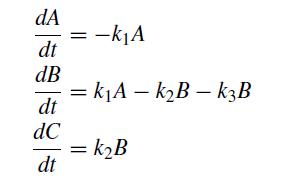
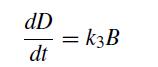
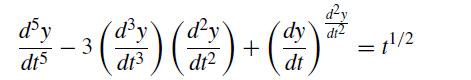
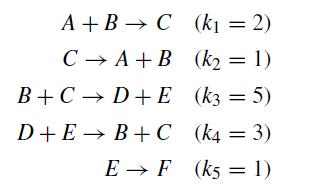
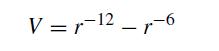
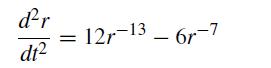
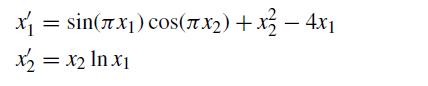
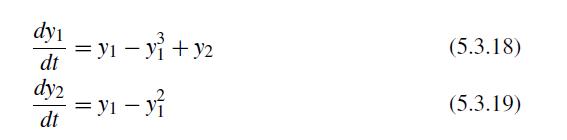
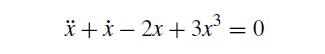
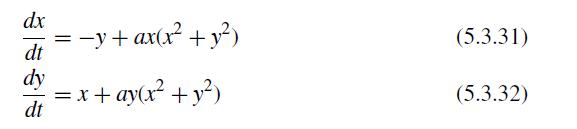
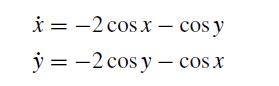
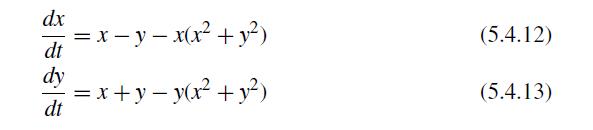
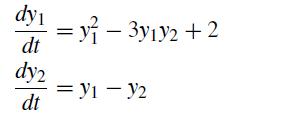
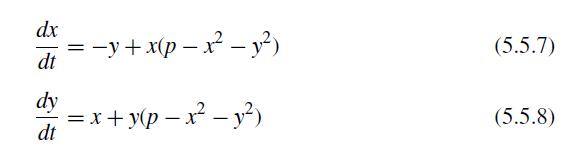
![et-y - 1 []=[] xy- +2 dt](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1697/6/9/2/1876530ba1b6ec3c1697692185114.jpg)
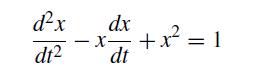
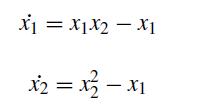
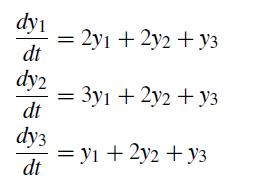
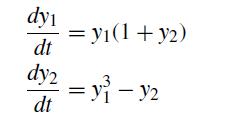
![P -]-[8] = 3-2 -3 2 X ][3] y](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1697/6/9/2/2766530ba748b49c1697692273638.jpg)
![[x2] = [ d dt X2 x + x2 x1 + x2](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1697/6/9/2/3166530ba9c5157e1697692313947.jpg)
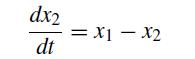
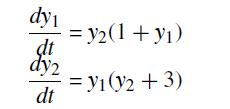
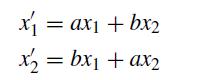
![J 13 - [18] a 0](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1697/6/9/2/3486530babc2d57e1697692345263.jpg)
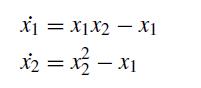
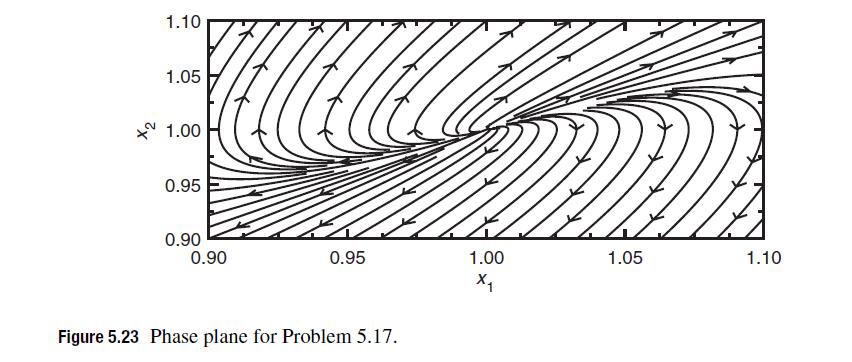
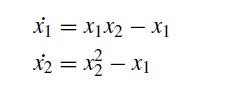
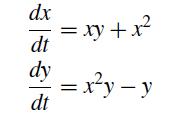
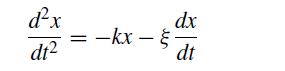
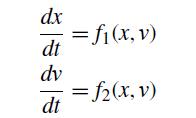
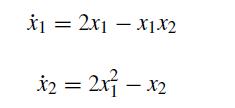
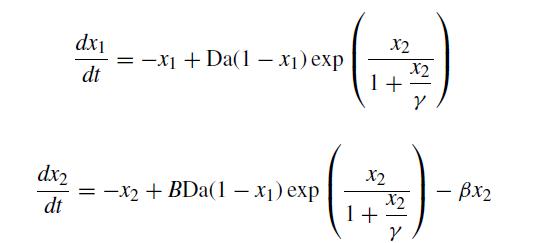
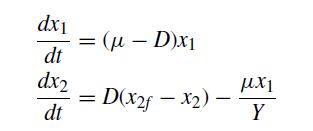
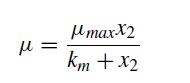
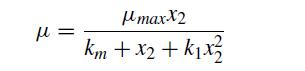
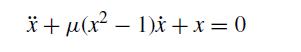
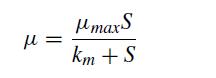
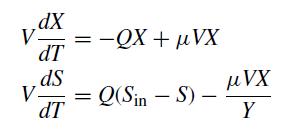
![d X # [] = [ dt y xy + sin y x(y - 1) ]](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1697/6/9/2/9226530bcfaabc621697692919884.jpg)