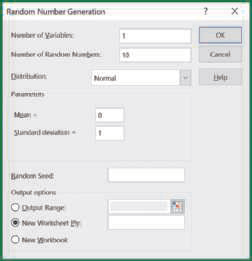
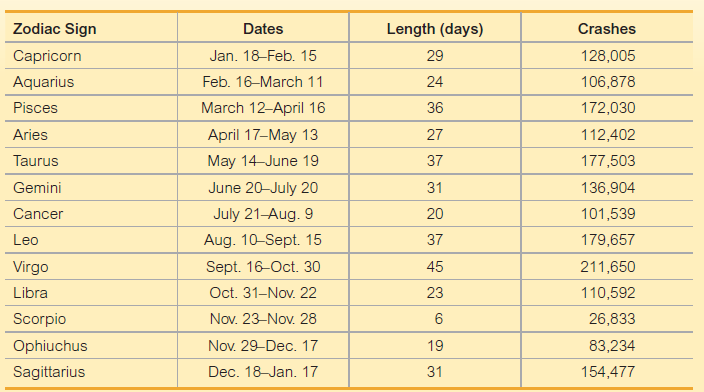
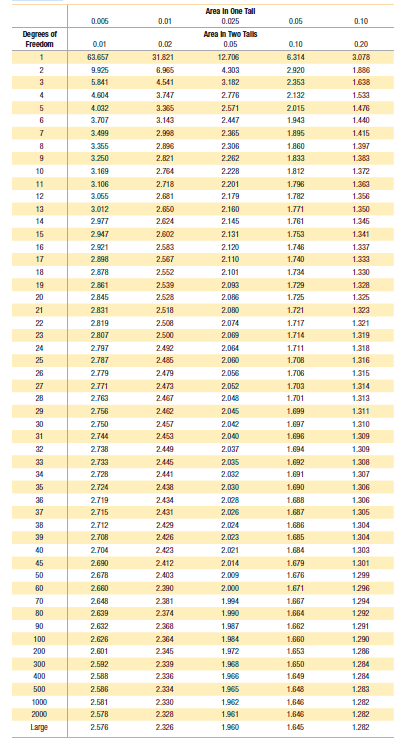
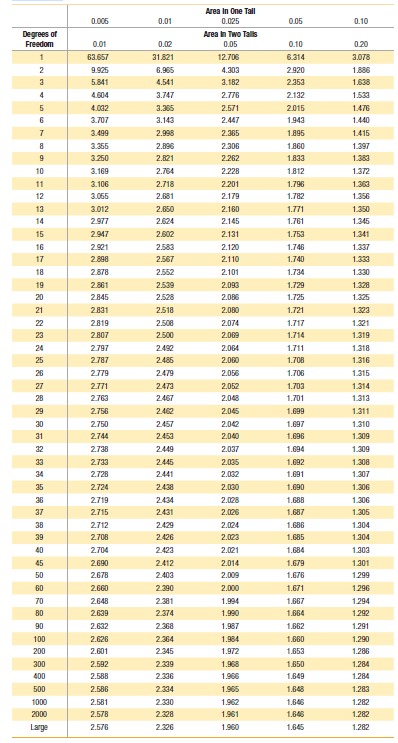
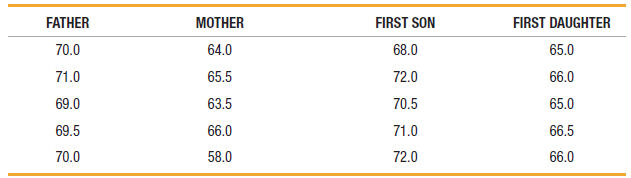
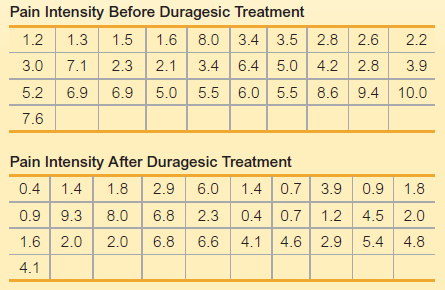
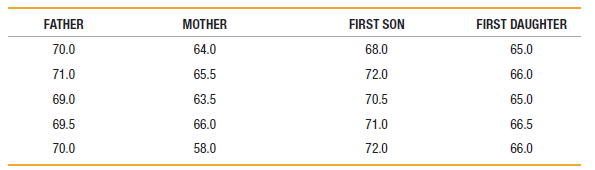
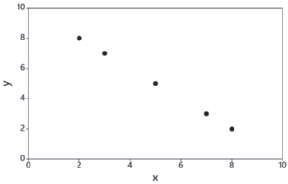
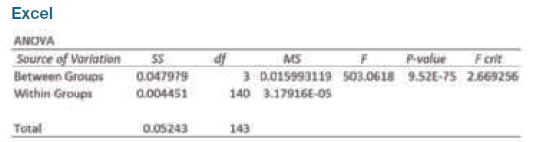
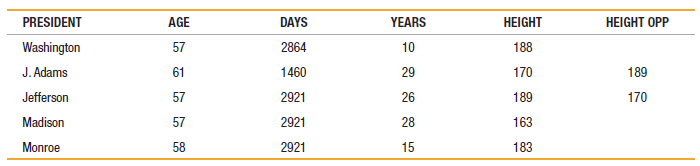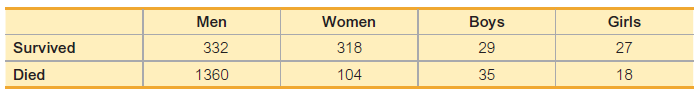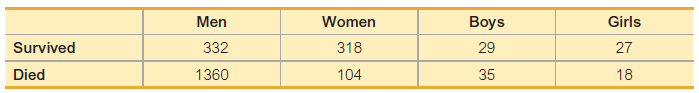Elementary Statistics Using Excel 6th Edition Mario F. Triola - Solutions

Discover the ultimate resource for mastering "Elementary Statistics Using Excel 6th Edition" by Mario F. Triola. Access a comprehensive collection of solved problems, answers key, and solutions pdf, all designed to enhance your understanding. With our step-by-step answers and chapter solutions, you'll find everything you need to excel in your statistics course. Our online solution manual and instructor manual provide detailed explanations, making it easier to tackle even the most challenging questions and answers. Explore the test bank and textbook solutions, all available for free download, and take your learning to the next level.