![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


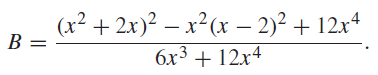
![[A], = [A],e, -kt](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/2/1/2/1145c1a10d214d821545194696082.jpg)
![[4], = [A], e¬k, –kt](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1545/2/1/0/6085c1a0af01b7d11545193190172.jpg)