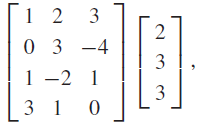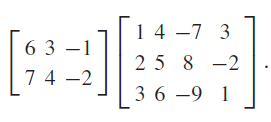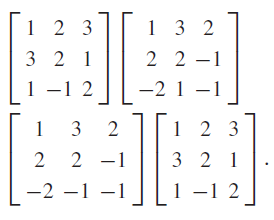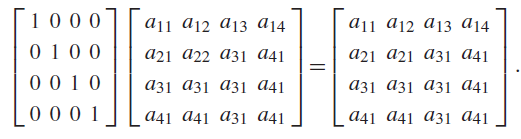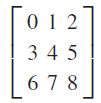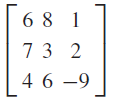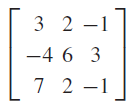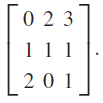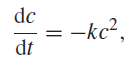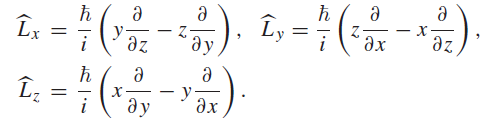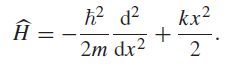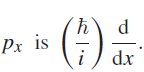![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


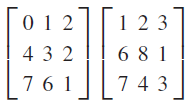
![6 3 2 -1 4 7 -6 –8 -7 4 3 2 3 -6 8 -6 1 3 2 -2 6 7 -1 -3]L-1 4 2 2 3 -3 4 3](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1546/0/8/6/7815c27697db28151546069380834.jpg)
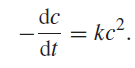

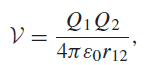
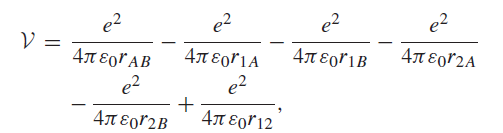
![2 3 [3 21 4] 3 -4 1 -2 1 0 1 3](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1546/0/8/6/8115c27699b0c3041546069410156.jpg)