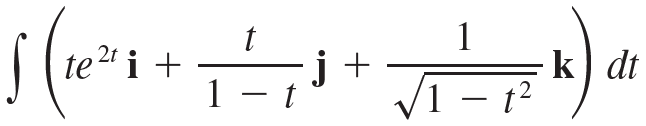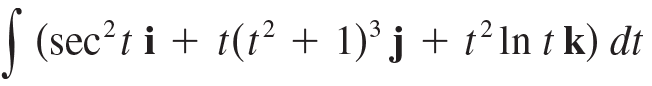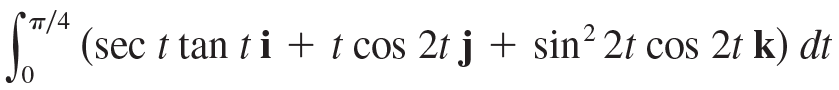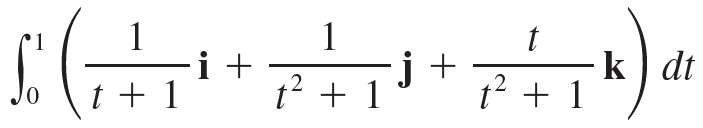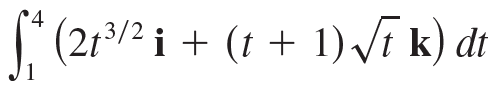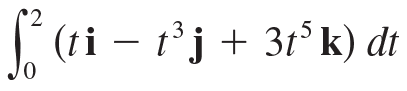![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


![[u(t) × v(t)] dt](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1552/7/5/3/8215c8d249d8320b1552736579965.jpg)
![[u(t) · v(t)] dt [(1)A](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1552/7/5/3/7785c8d247296eb81552736537111.jpg)