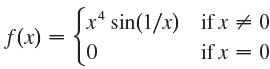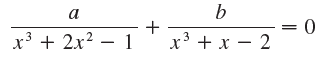![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


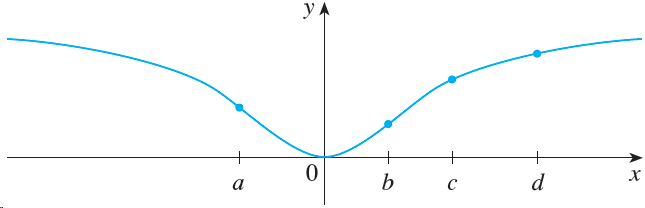
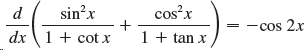
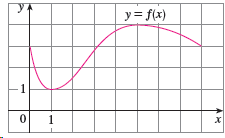
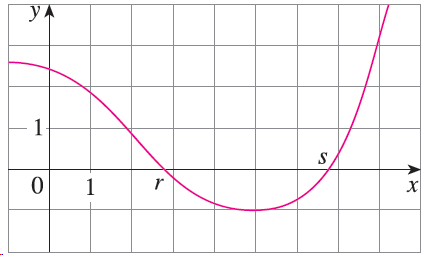
![deF(g(x))] = f](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1551/1/9/6/1795c756013ccf171551139294669.jpg)
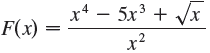
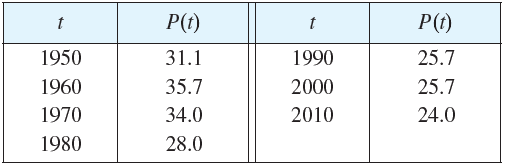
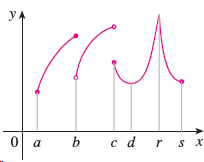
![g(x) [g(x)]? dx L g(x).](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1548/3/3/0/8605c49a76c0b7581548313511881.jpg)