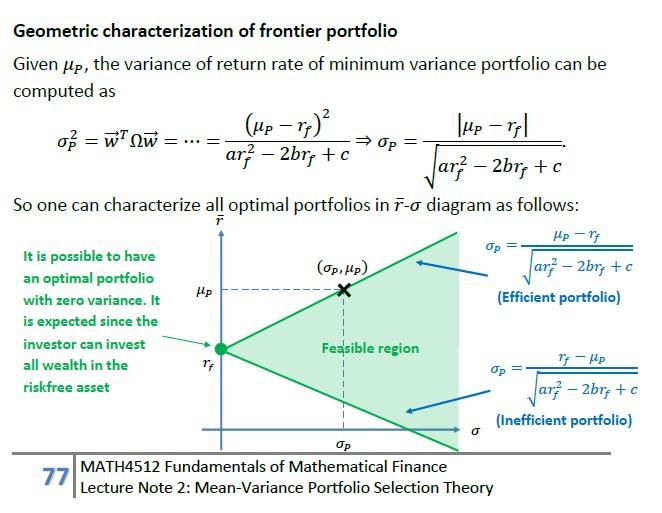
= = Bonus Problem 2 (Optional, 30 marks) We consider the mean variance portfolio selection with 1 riskfree asset and N risky asset (with N > 2) studied in the class. Given the target expected return chosen by the investor up, the investor chooses the portfolio which can minimize the variance. Recall that the optimal portfolio can be expressed as up -15 ---- - r;1) ary - 2bry + c up -15 w = 1 -(b - rra). ar; 2bry + c (a) Recall that the above formula is derived based on the first order condition in Lagrange method and the first order condition does not guarantee the optimality, show that the portfolio given by the formula is the desired optimal portfolio in the sense that for any other portfolio with the same expected return Mp, the variance of its return is always greater than that of the portfolio given by the above formula. (Hint: I have done the case for risky assets only. Try to study the proof and get some hint.) (b) In p.77, we see that the set of all portfolios (formed by these riskfree asset and risky assets) forms an infinite triangular which lies on the right of the frontier curve. Prove this statement mathematically. Op Geometric characterization of frontier portfolio Given up, the variance of return rate of minimum variance portfolio can be computed as o = WT 2w Tup - r| ar;} 2bre + c Jar} 2bry + c So one can characterize all optimal portfolios in F-o diagram as follows: - rf Op It is possible to have (op.up) an optimal portfolio ar; 2bry + c with zero variance. It Hp (Efficient portfolio) is expected since the investor can invest Feasible region all wealth in the If up Op riskfree asset ar; 2br + c (Inefficient portfolio) Op MATH4512 Fundamentals of Mathematical Finance 77 Lecture Note 2: Mean-Variance Portfolio Selection Theory TF = = Bonus Problem 2 (Optional, 30 marks) We consider the mean variance portfolio selection with 1 riskfree asset and N risky asset (with N > 2) studied in the class. Given the target expected return chosen by the investor up, the investor chooses the portfolio which can minimize the variance. Recall that the optimal portfolio can be expressed as up -15 ---- - r;1) ary - 2bry + c up -15 w = 1 -(b - rra). ar; 2bry + c (a) Recall that the above formula is derived based on the first order condition in Lagrange method and the first order condition does not guarantee the optimality, show that the portfolio given by the formula is the desired optimal portfolio in the sense that for any other portfolio with the same expected return Mp, the variance of its return is always greater than that of the portfolio given by the above formula. (Hint: I have done the case for risky assets only. Try to study the proof and get some hint.) (b) In p.77, we see that the set of all portfolios (formed by these riskfree asset and risky assets) forms an infinite triangular which lies on the right of the frontier curve. Prove this statement mathematically. Op Geometric characterization of frontier portfolio Given up, the variance of return rate of minimum variance portfolio can be computed as o = WT 2w Tup - r| ar;} 2bre + c Jar} 2bry + c So one can characterize all optimal portfolios in F-o diagram as follows: - rf Op It is possible to have (op.up) an optimal portfolio ar; 2bry + c with zero variance. It Hp (Efficient portfolio) is expected since the investor can invest Feasible region all wealth in the If up Op riskfree asset ar; 2br + c (Inefficient portfolio) Op MATH4512 Fundamentals of Mathematical Finance 77 Lecture Note 2: Mean-Variance Portfolio Selection Theory TF