Please show complete solution.

Review Example 2-5.

Suppose that you are commissioned to design a series of reactors that can achieve 65% conversion given the same reaction carried out adiabatically but are limited to using only two reactors, i.e. a CSTR and a PFR. Further, suppose that you have the option to choose any size of the two reactors and arranged in whatever configuration you find best for the situation.

What sizes of the reactors would you propose, how would they be arranged, and what is the intermediate conversion from this arrangement (or the conversion after the first reactor)?

What would your argument be comparing this set up with the original one consisting of three reactors, i.e. is it worse, better, or the same as the first? List down the assumptions you have made to come up with the reactor configuration.

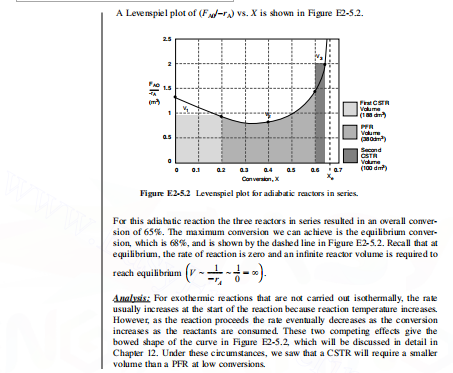
Exanple 2-5 An Adiabatic LiquidPhase Isounerization The isomerization of butane nC4H10iC4H10 was carried out adiabatically in the liquid phase. The data for this reversible reaction are given in Table E2-5.1. (Example 11.3 shows how the data in Table E2-5.1 were gener ated.) Don't worry how we got this data or why the (1/rA) looks the way it does; we will see how to construct this table in Chapler 11, Example 11-3. It is real data for a real rection carried out adiabatically, and the reactor scheme shown below in Figure F2.5.1 is used. Figure E.2.5.1 Reactors in series. Calculate the volume of each of the reactors for an entering molar flow rate of n-butane of 90kmol/hr. Solution Baking the reciprocal of rA and multiplying by FA0, we obtain Table E2-5.2. E.g. at X=0:rAFs0=39kmoV/hm390kmol/h=1.28m3 Tann E2-5.2 Pioocesen Datat + Data from Table E11.3.1. (a) For the first CSTR, when X=0.2, then rAFAO=0.94m3 V1=rAFAOX1=(0.94m3)(0.2)=0.18.m3V1=0.188m3=18.dm3 (b) For the PFR, V2=a2a6(rAF0)dX Using Simpson's three-point formula with X=(0.60.2)/2=0.2, and X1=0.2, X2=0.4, and X3=0.6 Rearranging V3=rASFS2FA3FA2=FA0FA0X2FA3=FA0FA0X3V3=rA3(FA0FSAX2)(FS0FA0XS) Simplifying Vs=(rASFM0)(X3X2) We find from Table E2-5.2 that at X3=0.65, then rAsFS0=2.0m3 V3=2m3(0.650.6)=0.1m3V3=0.1m3100dm3 A Levenspiel plot of (F/rA) vs. X is shown in Figure E2-5.2. Fagure Ezes.2 Levenspuel plot tor adiabatw reactors an serves. For this adiabatic reaction the three reactors in series resulted in an overall conversion of 65%. The maximum conversion we can achieve is the equilibrium conversion, which is 68%, and is shown by the dashed line in Figure E2-5.2. Recall that at equilibrium, the rate of reaction is zero and an infinite reactor volume is required to reach equilibrium (VrA101). Amalyais: For exothermic reactions that are not carried out isothermally, the rate usually increases at the start of the reaction because reaction temper ature increases. However, as the reaction proceeds the rate eventually decreases as the conversion increases as the reactants are consumed. These two competing effects give the bowed shape of the curve in Figure E2-5.2, which will be discussed in detail in Chapver 12. Under these circumstances, we saw that a CSTR will require a smaller volume than a PFR at bow conversions