using matlab. Answer questions below

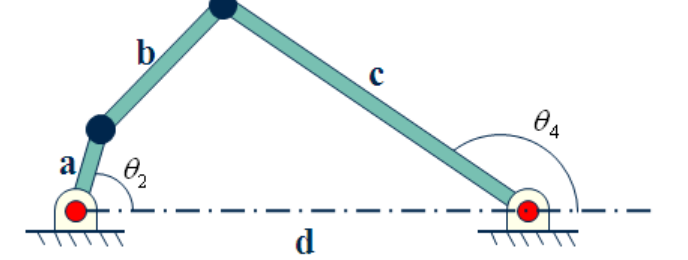
A four-bar linkage system is shown above. The first link, a, is an input link (crank) of length 1. The second link, b, is a coupler link of length 2. The third link, c, is an output link of length 4. The forth link, d, is the fixed link (ground) of length 5. All lengths are provided in metres.The angular position of the output link (4) of a four-bar linkage corresponding to the angular position of the input link (2) can be computed using the Freudensteins equation: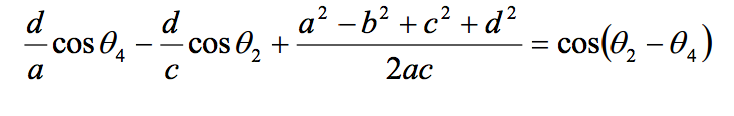

The following parameters must be used for root finding: xl = 120, xu = 165, xi = 120, pert = 0.01, precision = 1e-4.

1. Write an m-file to find the value of 4 for 2=30 using fzero.

2. Check this result using the bisection, false position and modified secant methods. For each method use fprintf to print the root and the number of iterations each method takes. Use fprintf to print a statement mentioning which method requires the last amount of iterations.

3. Plot the absolute difference between the estimated root and the actual root (i.e. 0) for each method against the respective number iterations on the same plot. Remember to label the plot with a legend.

b c a a b c a a