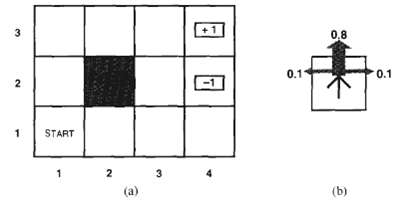
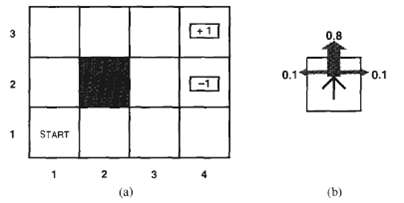
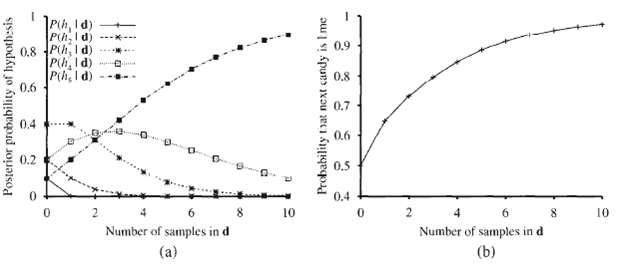
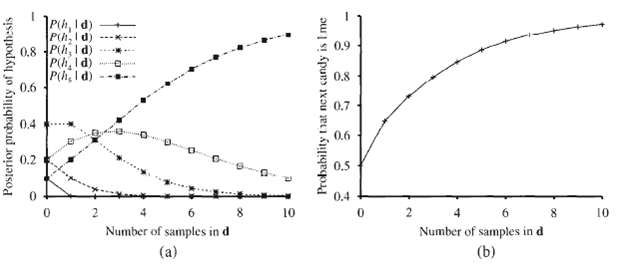
![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()




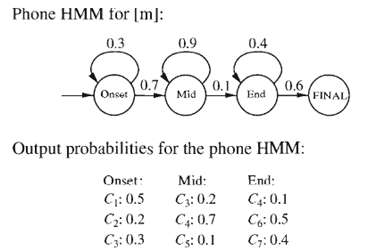
![(a) Word model with dialect variation: (eyl 0.5 1.0 1.0 1.0 (ow] 1.0 (t) [m] [ow] (1) 1.0 (aa] (b) Word model with coart](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1548/9/1/1/7625c5284922872d1548911763509.jpg)