A closed-loop system is shown below. The noise transfer function (frac{C_{n}(s)}{N(s)}left[C_{n}(s)= ight.) output corresponding to noise input (mathrm{N}(mathrm{s})) ] is approximately: (a) (frac{1}{mathrm{G}(s) mathrm{H}_{1}(s)})

A closed-loop system is shown below. The noise transfer function \(\frac{C_{n}(s)}{N(s)}\left[C_{n}(s)= \right.\) output corresponding to noise input \(\mathrm{N}(\mathrm{s})\) ] is approximately:

(a) \(\frac{1}{\mathrm{G}(s) \mathrm{H}_{1}(s)}\) for \(\left|\mathrm{G}(s) \mathrm{H}_{1}(s) \mathrm{H}_{2}(s) \right| \)

(b) \(-\frac{1}{\mathrm{H}_{1}(s)}\) for \(\left|\mathrm{G}(s) \mathrm{H}_{1}(s) \mathrm{H}_{2}(s) \right|>>1\)
(c) \(-\frac{1}{\mathrm{H}_{1}(s) \mathrm{H}_{2}(s)}\) for \(\left|\mathrm{G}(s) \mathrm{H}_{1}(s) \mathrm{H}_{2}(s) \right|>>1\)
(d) \(-\frac{1}{\mathrm{G}(s) \mathrm{H}_{1}(s) \mathrm{H}_{2}(s)}\) for \(\left|\mathrm{G}(s) \mathrm{H}_{1}(\mathrm{~s}) \mathrm{H}_{2}(\mathrm{~s}) \right|\)

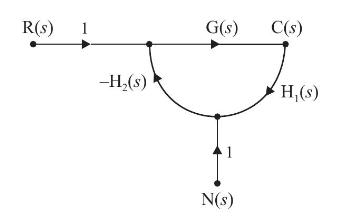
R(S) -H(s) G(s) C(s) 1 N(S) H (s)