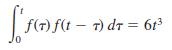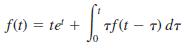![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


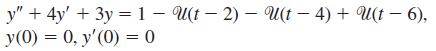
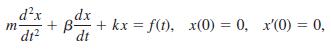
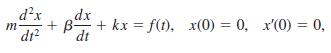
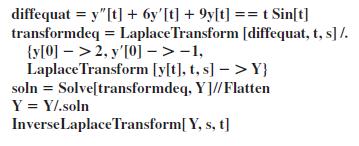
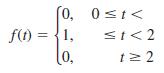
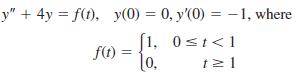
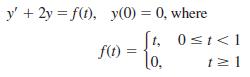
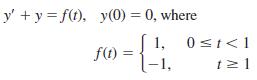
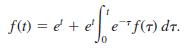
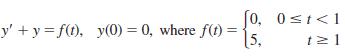
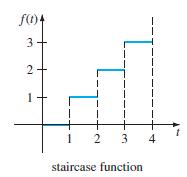
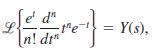
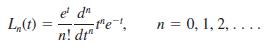
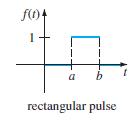
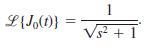
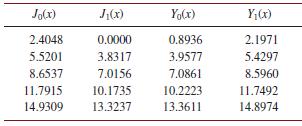
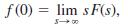

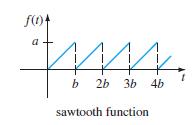
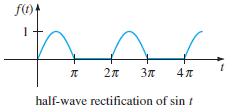
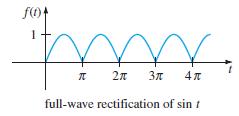
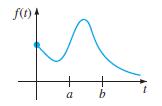
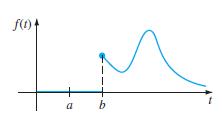
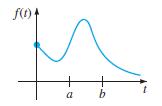
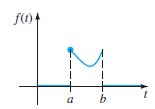
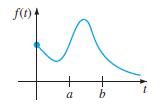
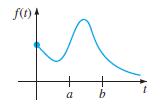
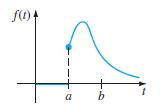
![L - In s+1]](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1601/5/2/8/1065f75612a9d3c11601528105768.jpg)
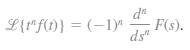
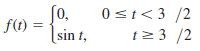
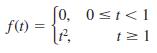
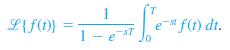
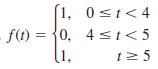
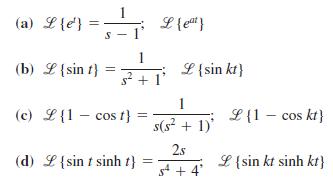
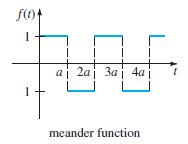
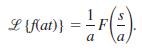

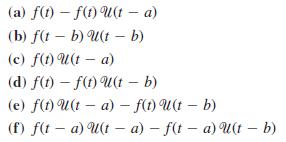
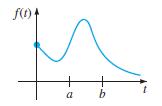
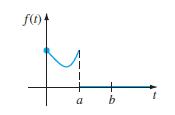
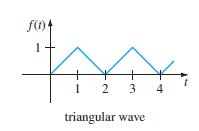
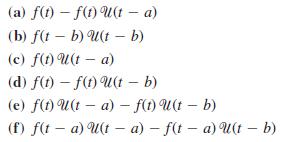
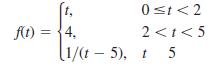
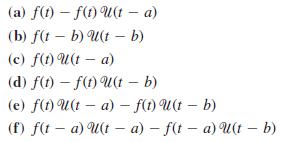
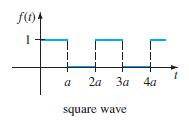
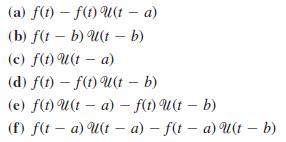
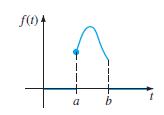
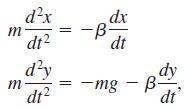
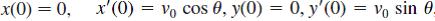
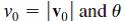
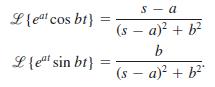
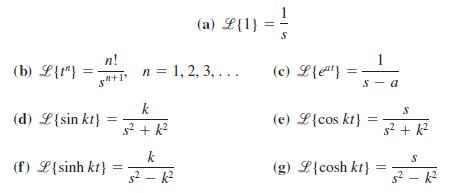
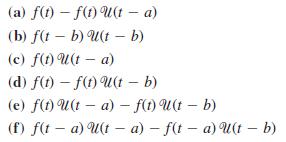
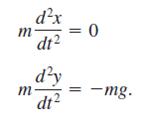
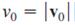
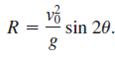
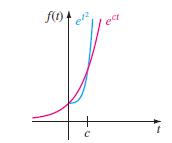
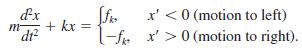
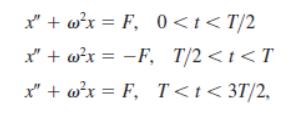
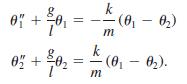
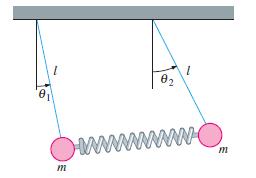
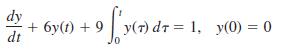
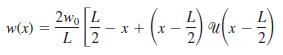
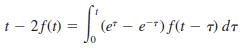
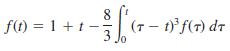
![S - a eal cos bt (s - a)? + b? b L(s - a) + b] eat sin bt.](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1601/4/5/8/5725f74518c5221e1601458579365.jpg)