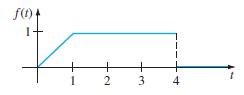
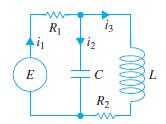
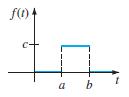
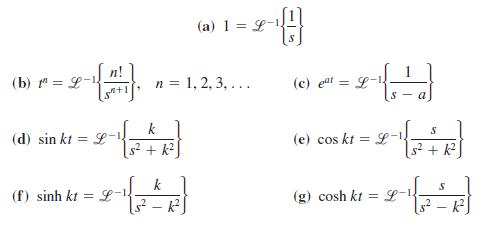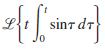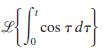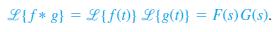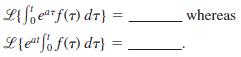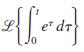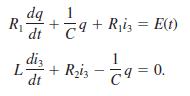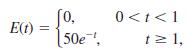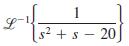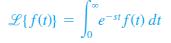![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


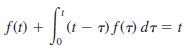
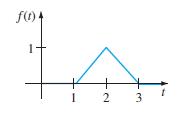
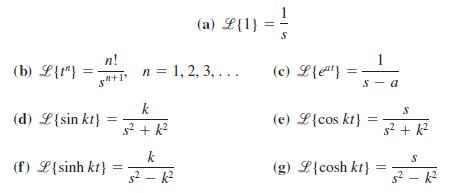
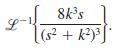
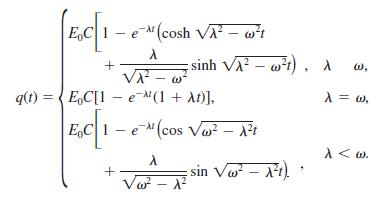
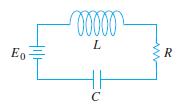

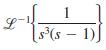
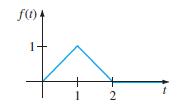
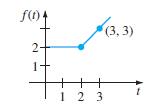
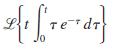
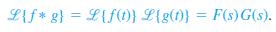
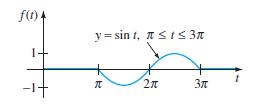
![6s + 3 L-1 s + 5s? + 4]](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1601/4/5/1/6465f74367e85a1c1601451647549.jpg)