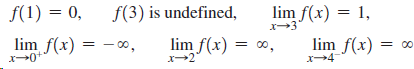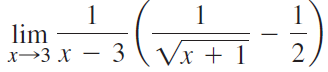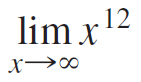![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


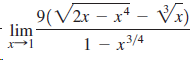
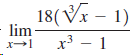
![УА х y = [x] -3 2.](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1548/1/5/9/0485c470848cb1fc1548141697060.jpg)
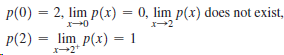
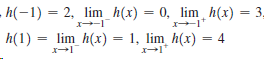
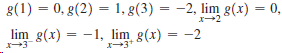
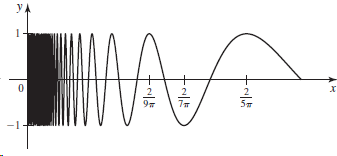
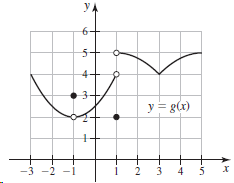
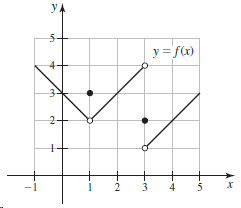
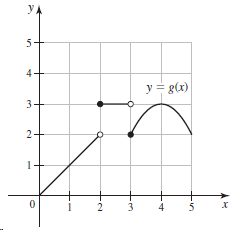
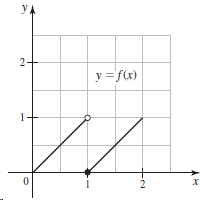
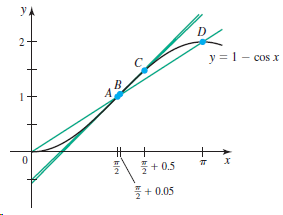


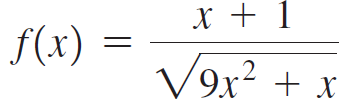
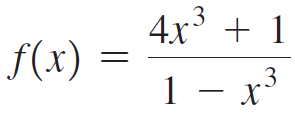
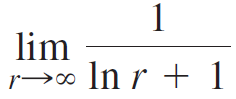
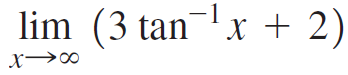
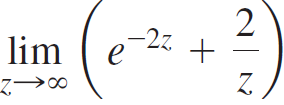
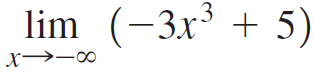
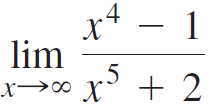
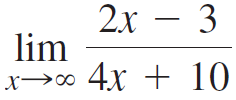
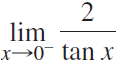
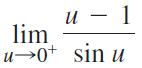
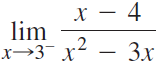
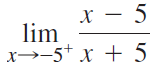
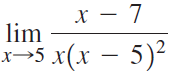
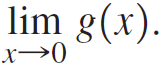
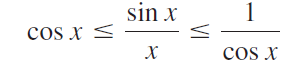
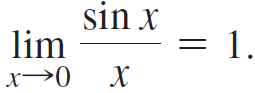
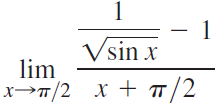
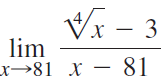
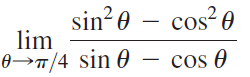
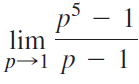
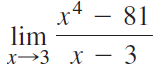
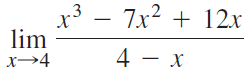
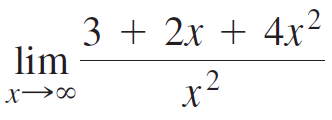
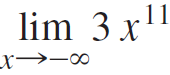
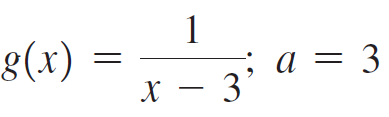
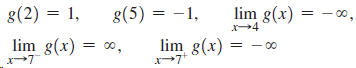
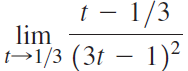
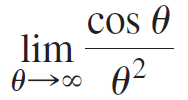
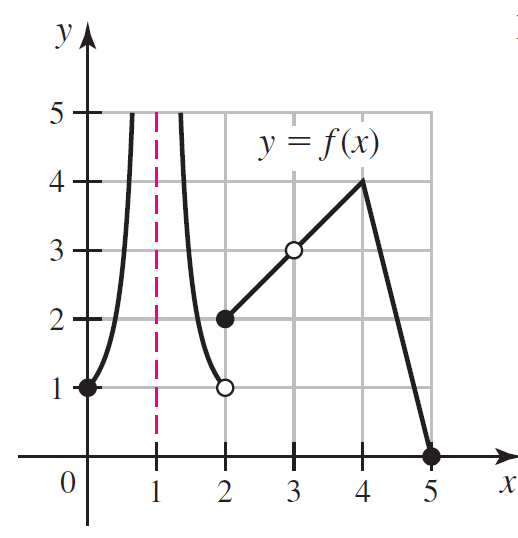
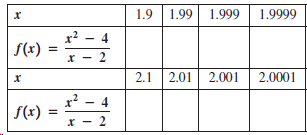
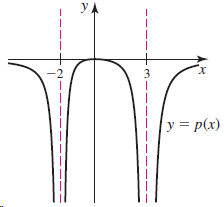
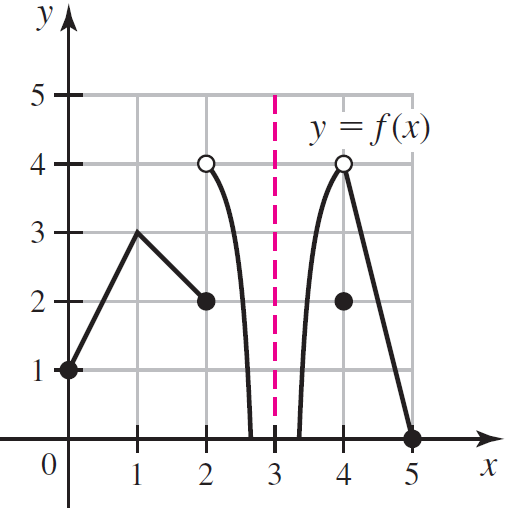
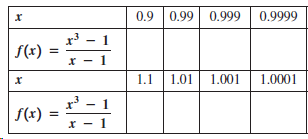
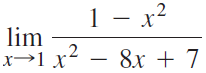
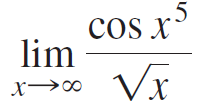
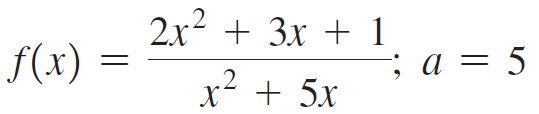
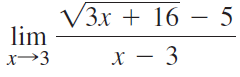
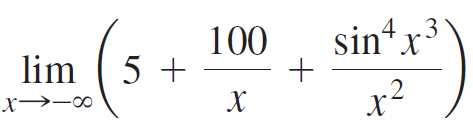
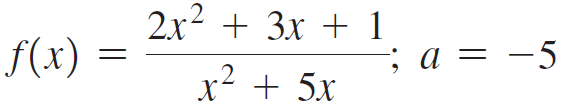
![Time interval [1,2] [1, 1.5] [1, 1.1] [1, 1.01]| [1, 1.001] Average velocity](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1548/1/4/8/9905c46e0fea0f8b1548131639187.jpg)