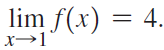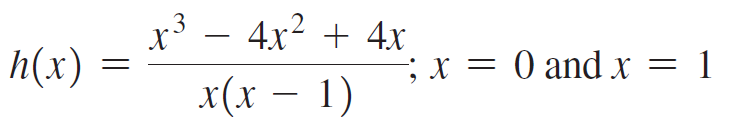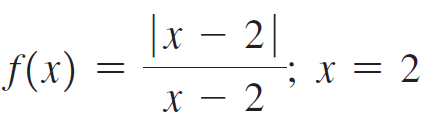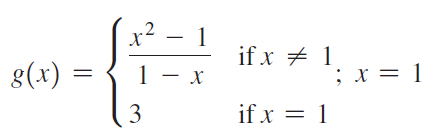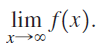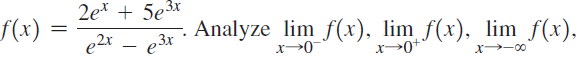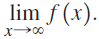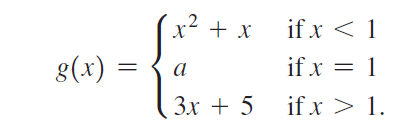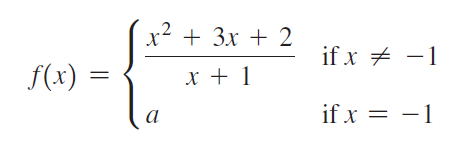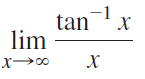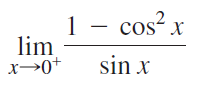![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


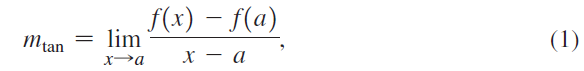
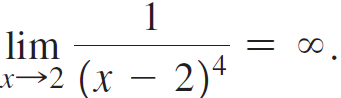
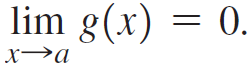
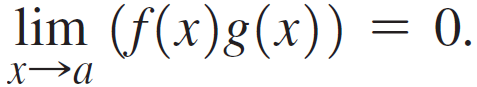
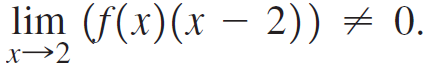
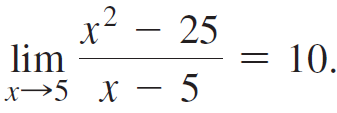
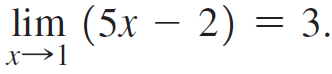
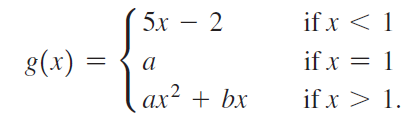
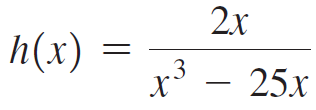
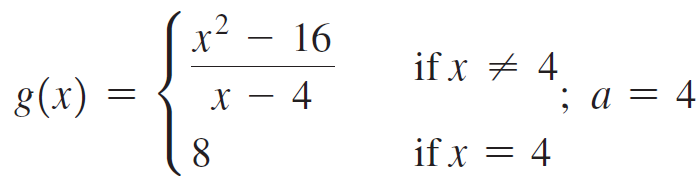
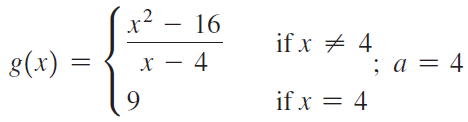
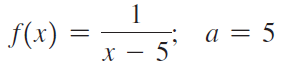
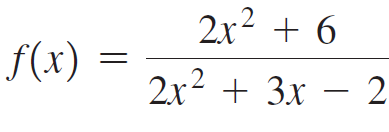
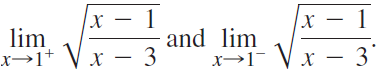
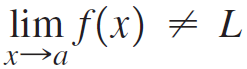
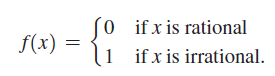
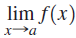
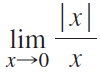
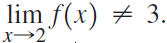
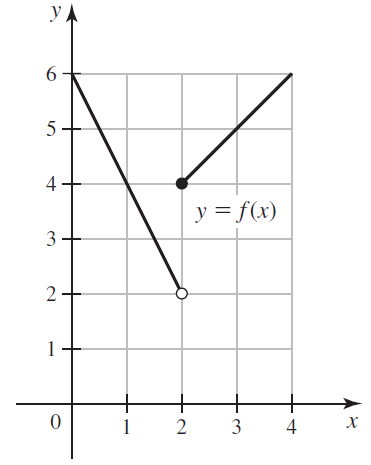
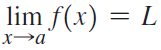
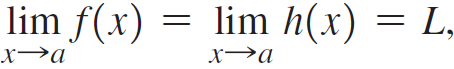
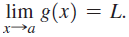
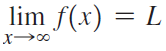
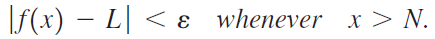
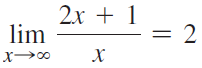
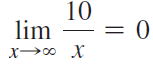
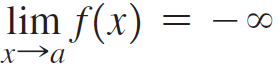
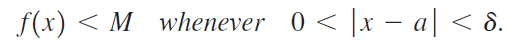
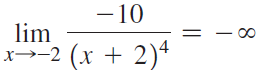
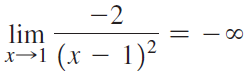
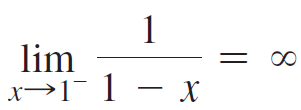
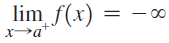
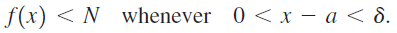
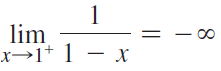
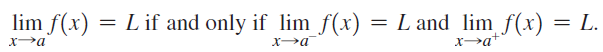
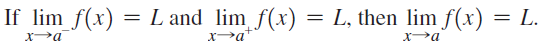
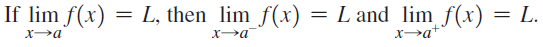
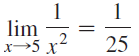
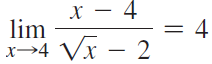
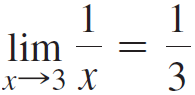
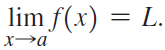
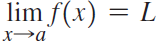
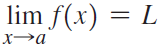
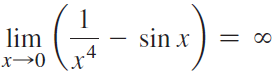
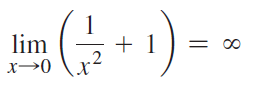
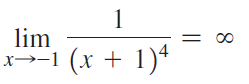
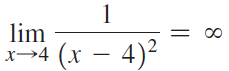
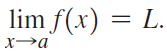
![lim [cf(x)] = cL,](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1548/9/4/1/1175c52f73d8bac81548923785676.jpg)