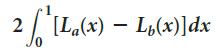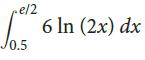![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


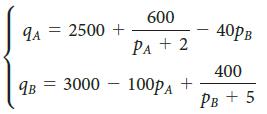

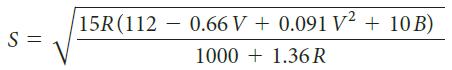

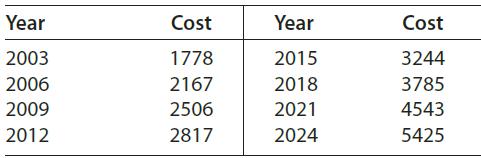
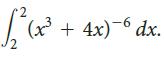
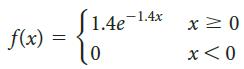
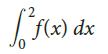
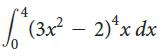
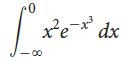
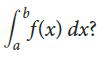
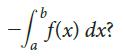
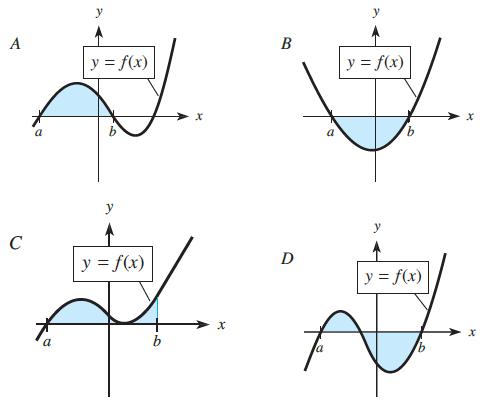
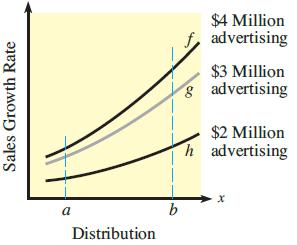
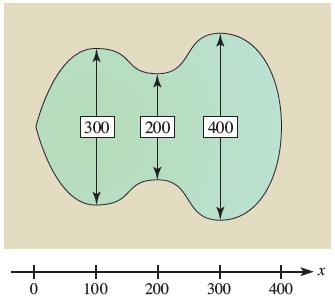
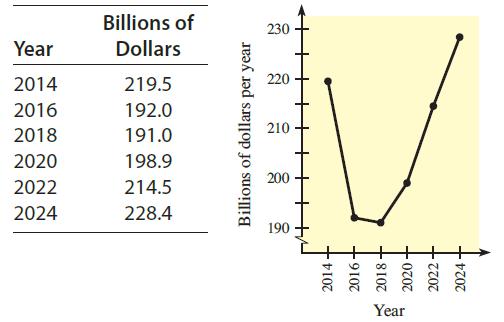
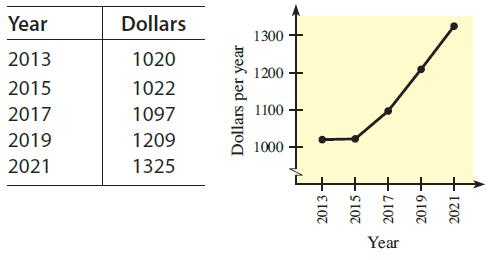
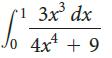
![2 (L.(x) – L(x)]dx L,(x)]dx](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1605/0/7/9/0085fab8fe0bed461605079016154.jpg)
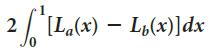
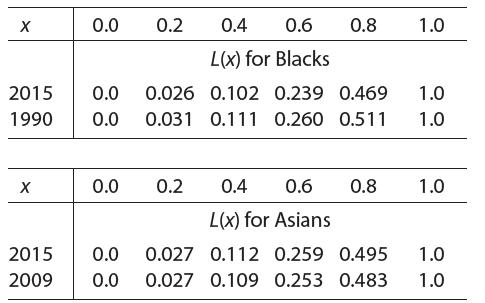
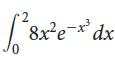
![2/ ILa(x) – L6(x)]dx](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1605/0/7/8/8235fab8f27bafc31605078831148.jpg)