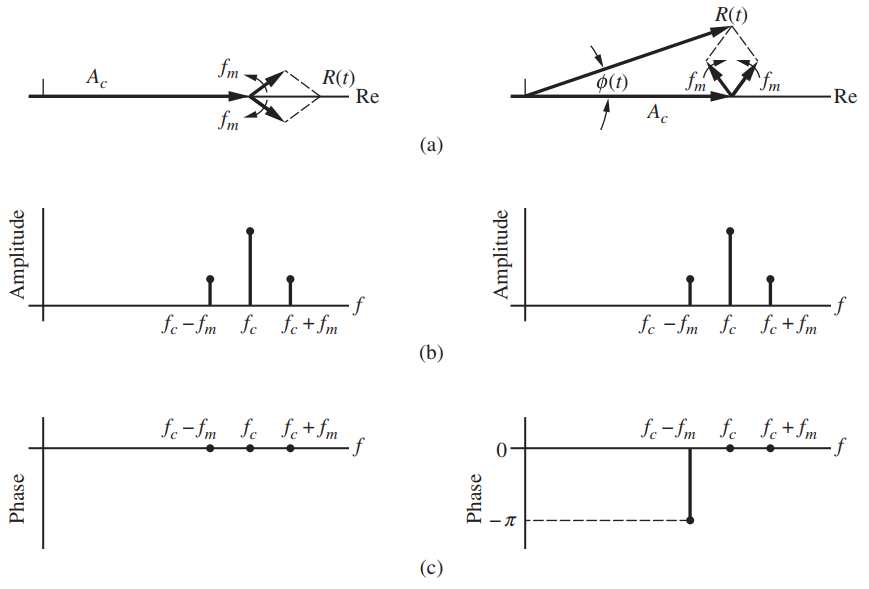
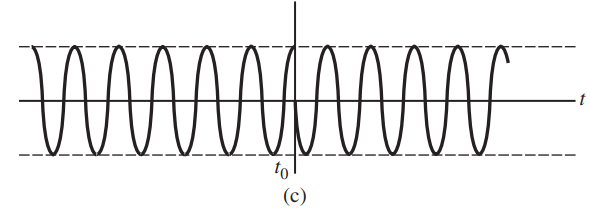
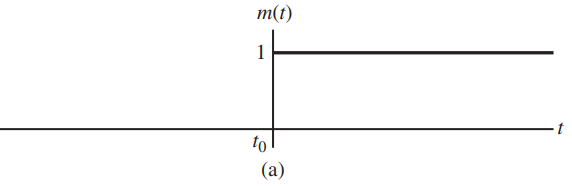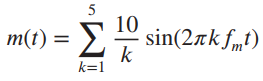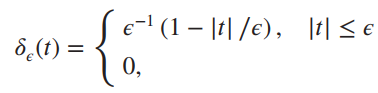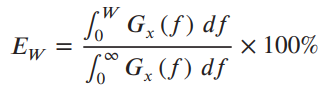![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


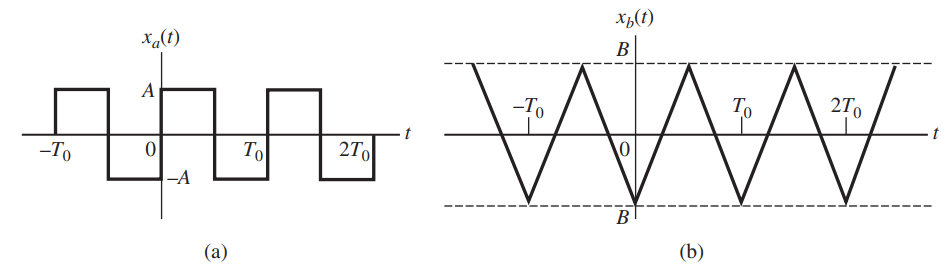
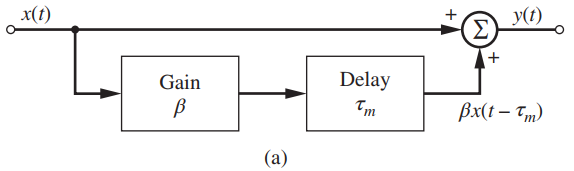
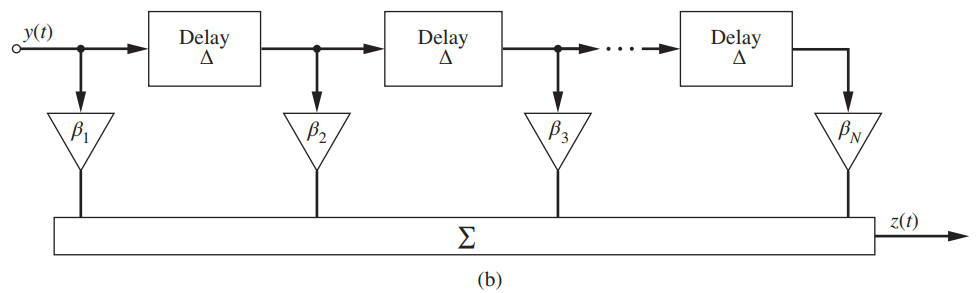
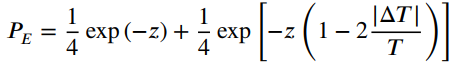
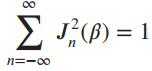
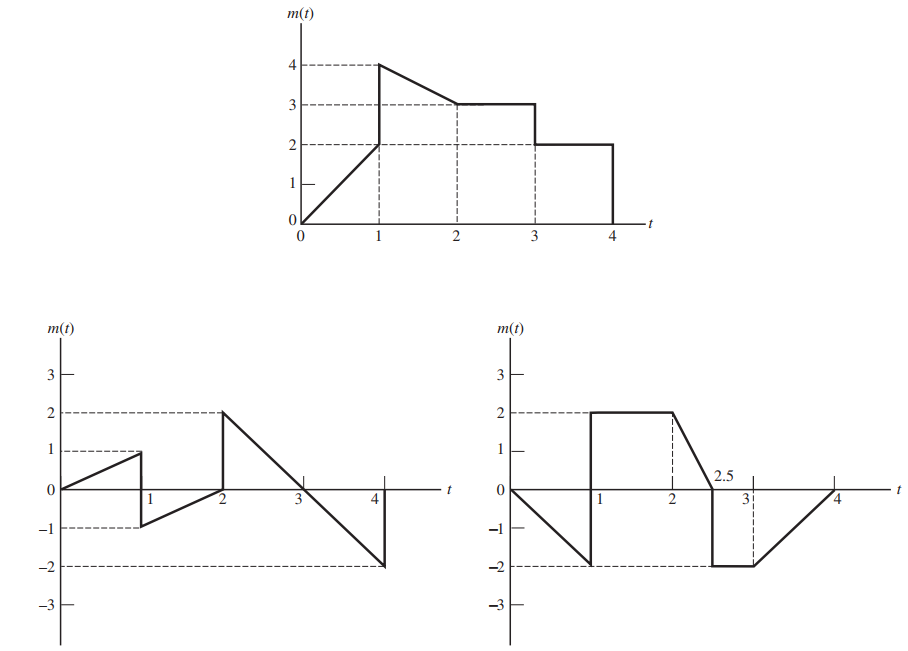
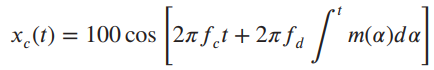
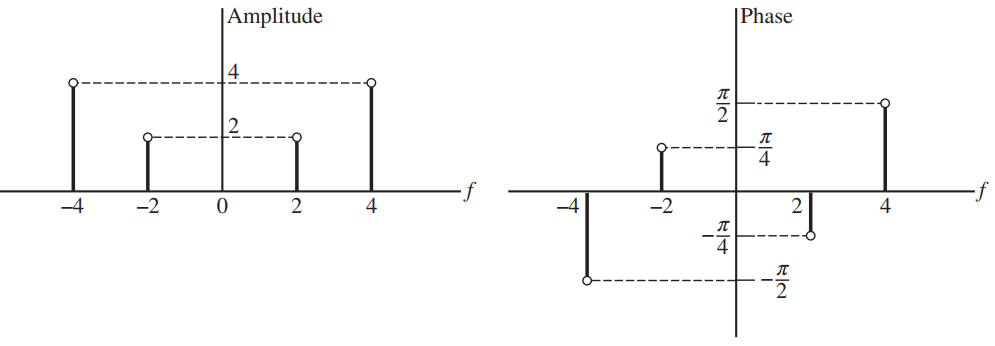
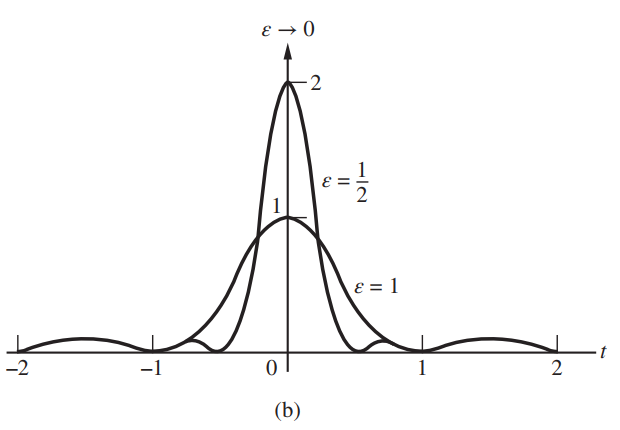
![AL2(B)| AHo($)] AV¿(B[ AV4B)| AdL3(B)| AV_4(B)| f (a) (b) Phase, rad Amplitude](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1536/9/2/0/8765b9b8d2c7fd1c1536903228111.jpg)