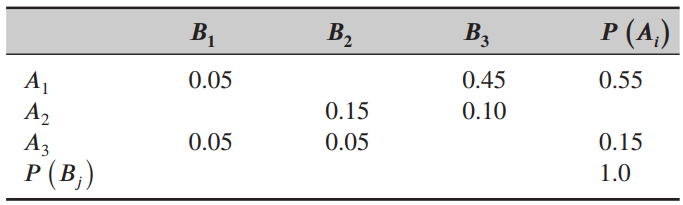
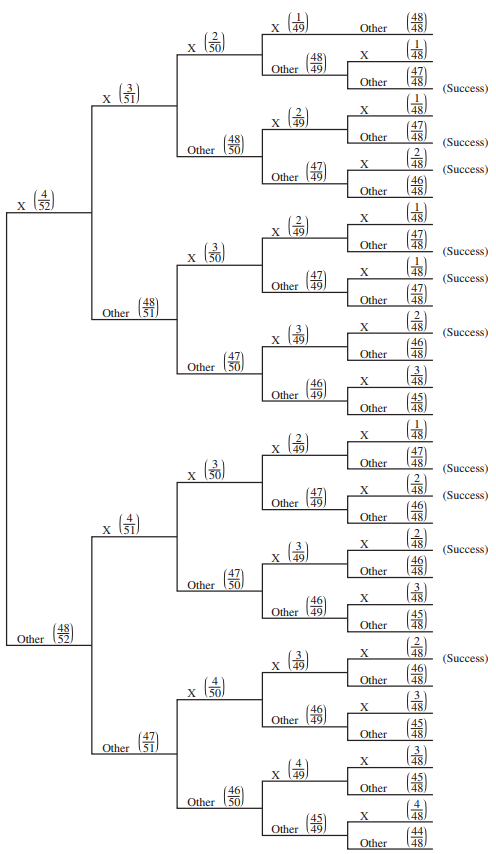
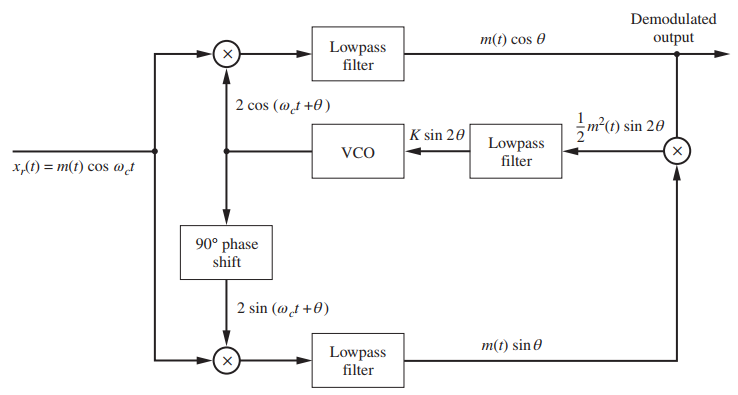
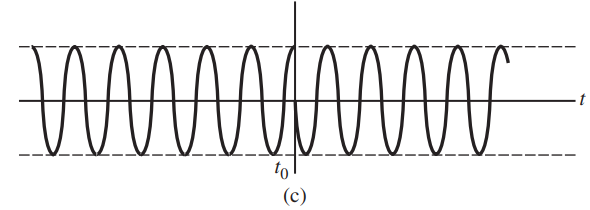
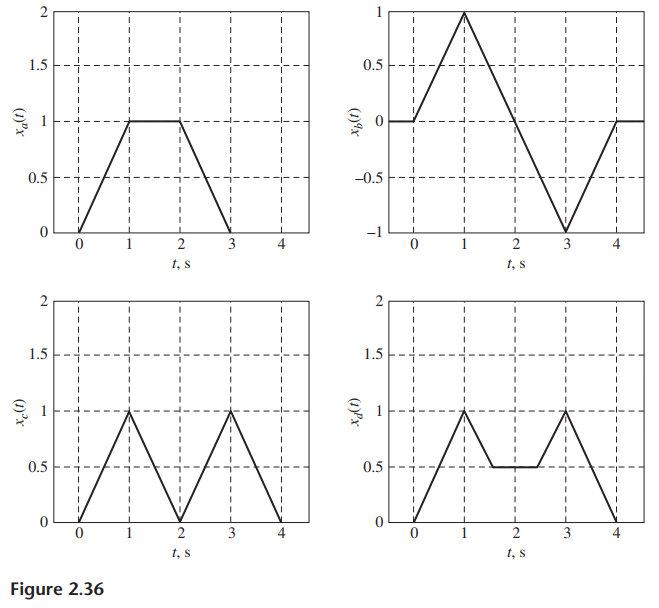
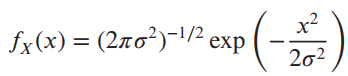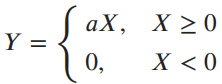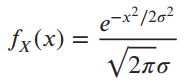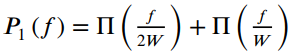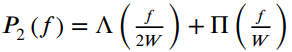![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


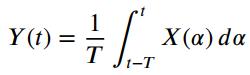
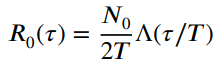
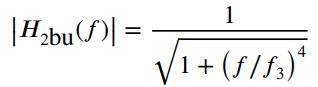
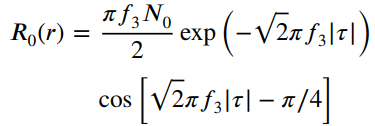

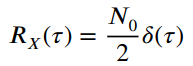
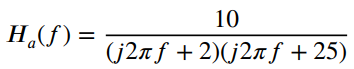
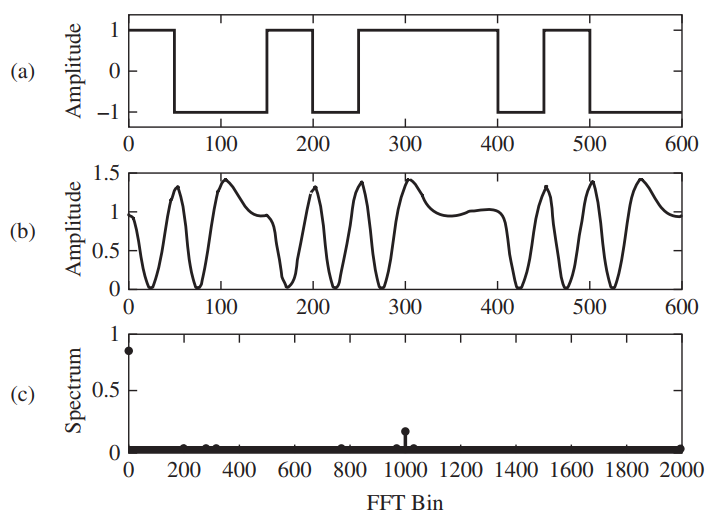
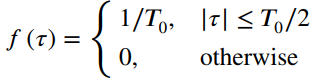
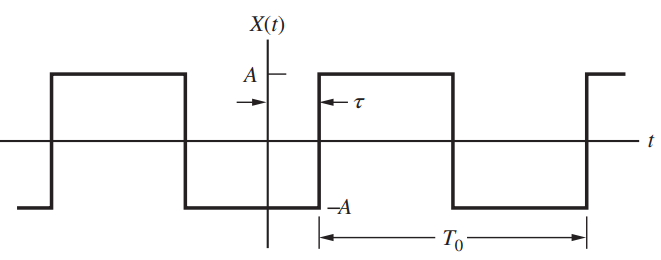
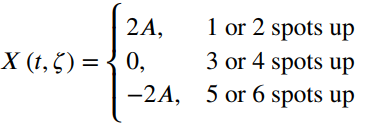
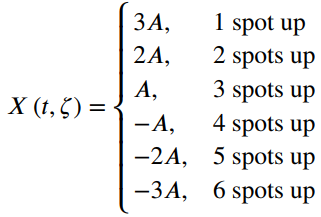
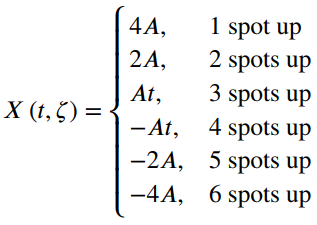
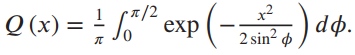
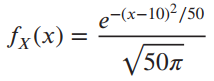

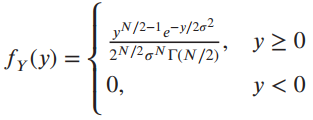
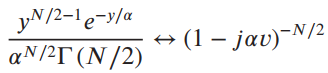
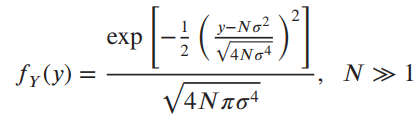
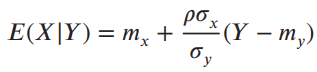
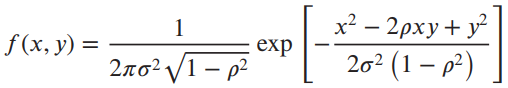
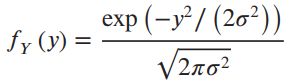
![fx(x) = ;5(x – 5) + lu(x – 4) – u(x – 8)]](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1537/3/5/2/4295ba222ed06c6b1537334794358.jpg)