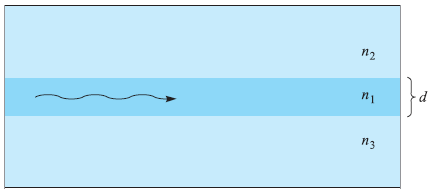
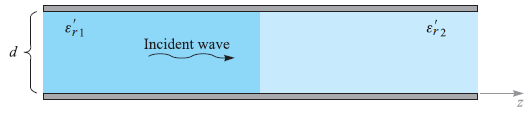
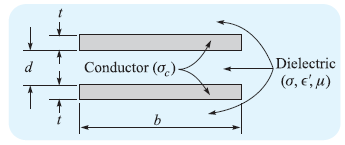
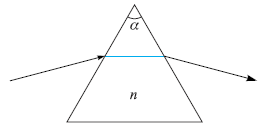
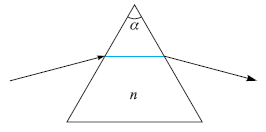
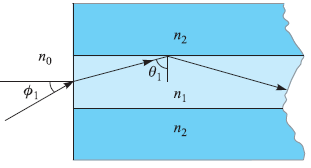
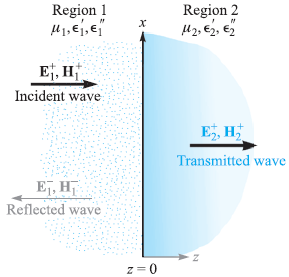
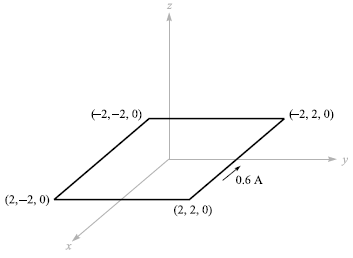
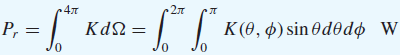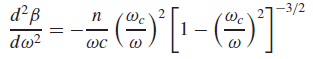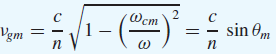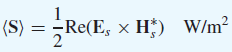![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


![7!/2 Iokd sin 0 exp[-j(kr Hos – 84)] 1+ (kr)? 4πr](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1537/6/0/8/6225ba60bae3a5021537590995604.jpg)
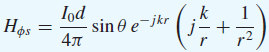
![יניו 1/2 Iod n|1+ 2n r2 cos 0 exp[- j(kr Ers – 8,)] (kr)2](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1537/6/0/8/4985ba60b32e65eb1537590872321.jpg)
![1/2 Iokd n|1 4πε (kr)² sin 0 exp[-j(kr – 80)] Ees (kr)4](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1537/6/0/8/5125ba60b40199f01537590885494.jpg)