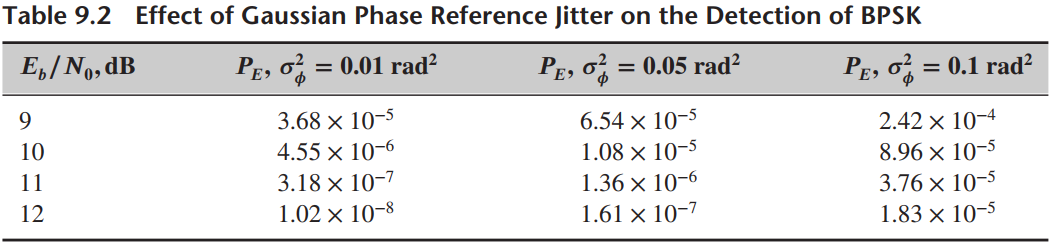
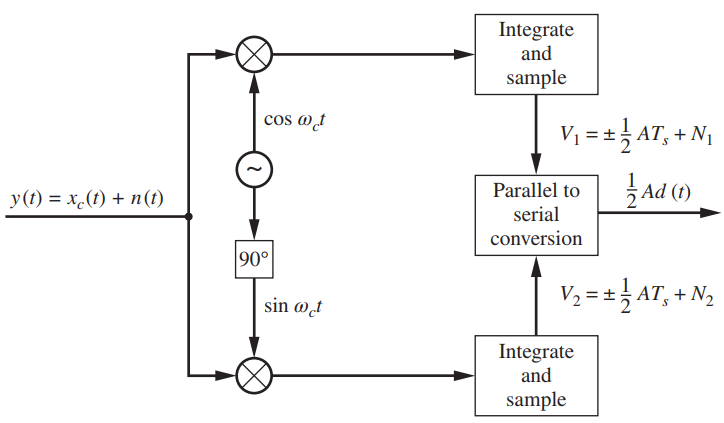
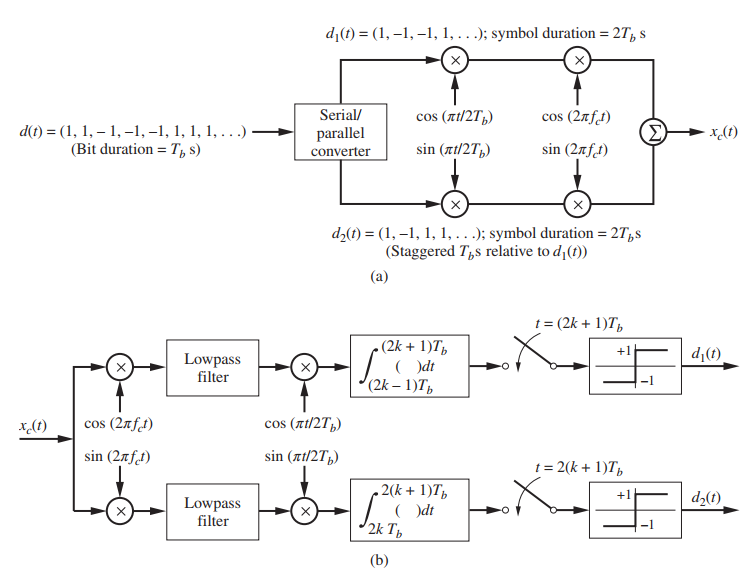
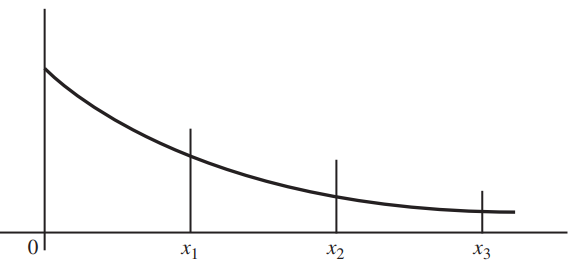
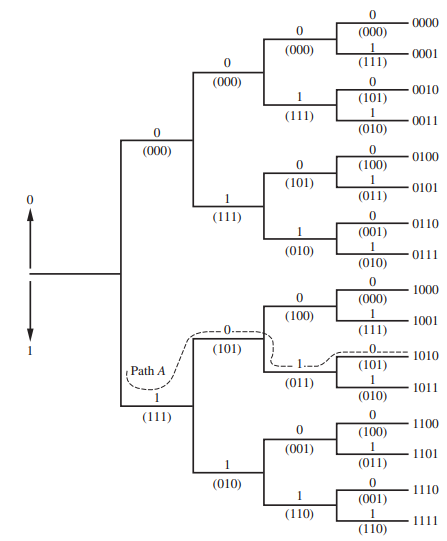
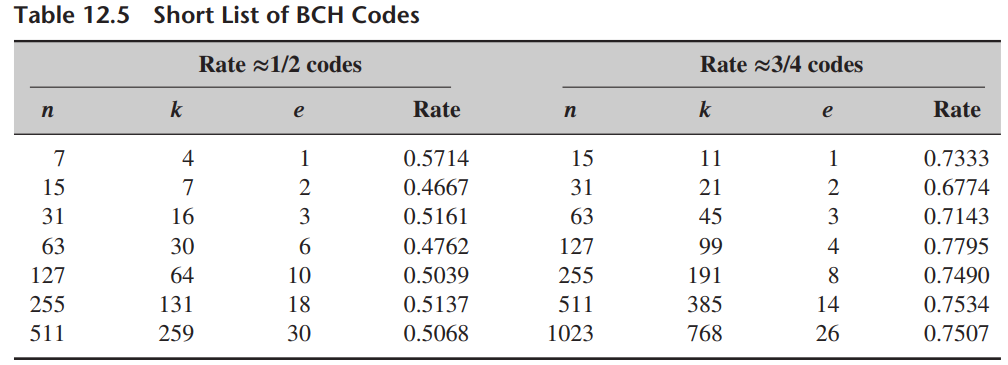
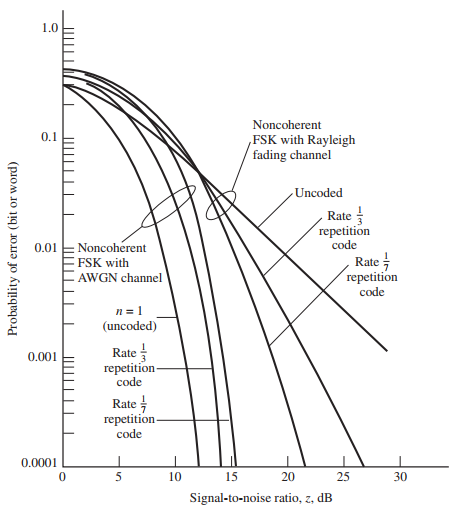
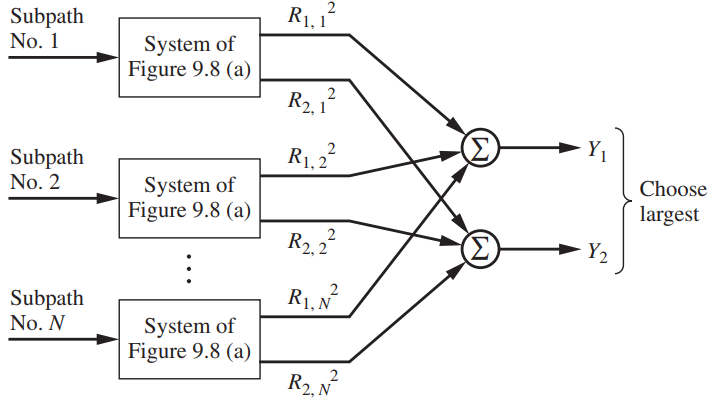
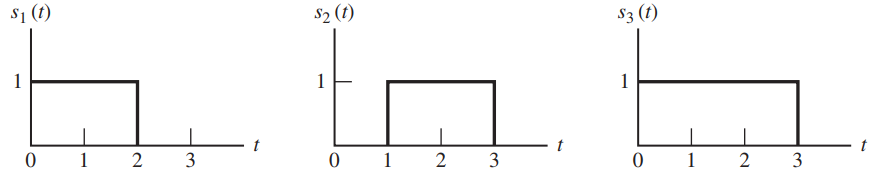
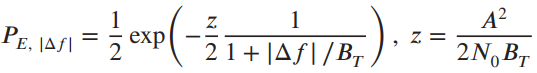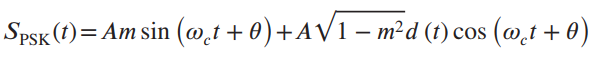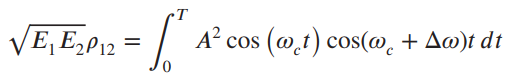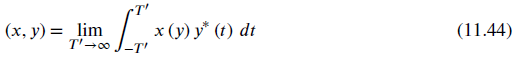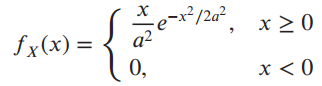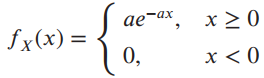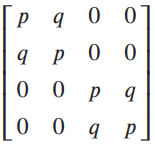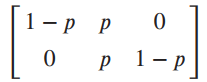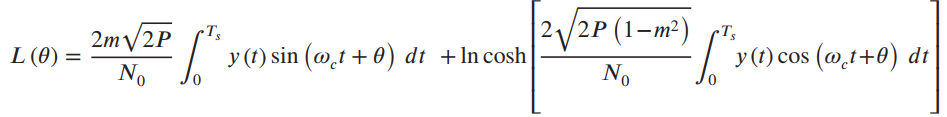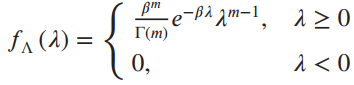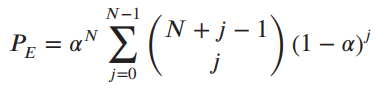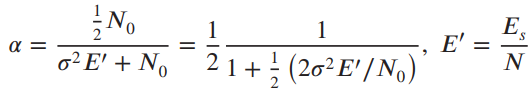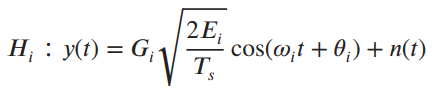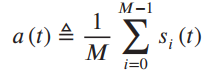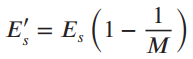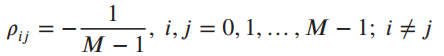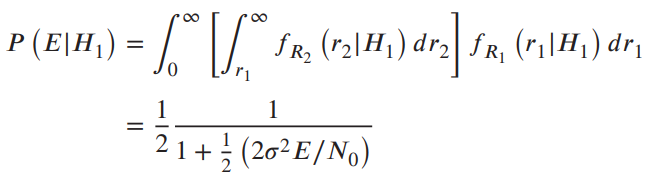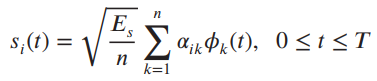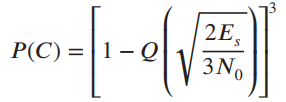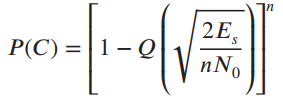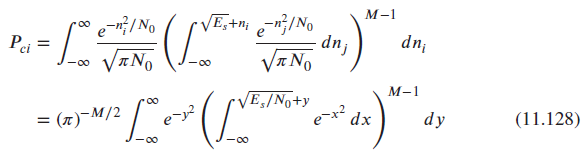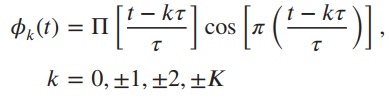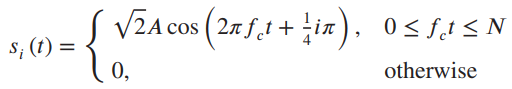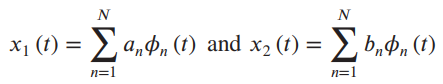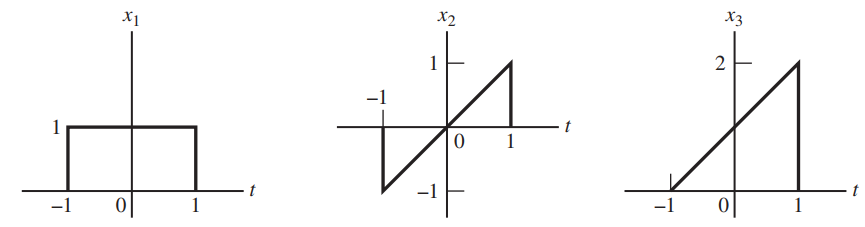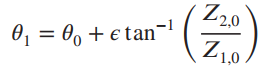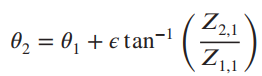![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


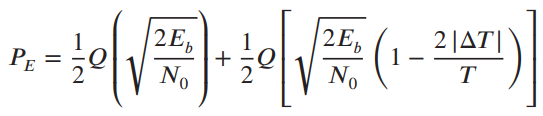
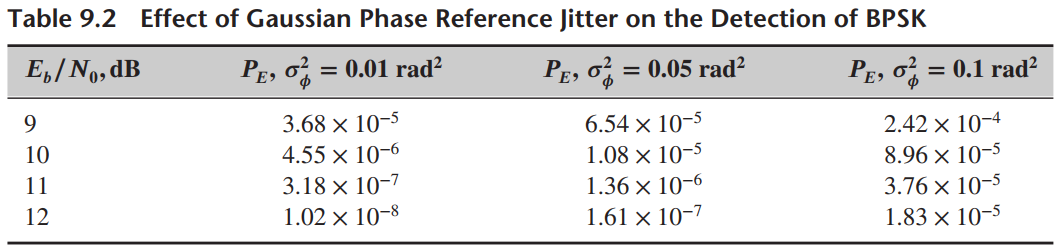
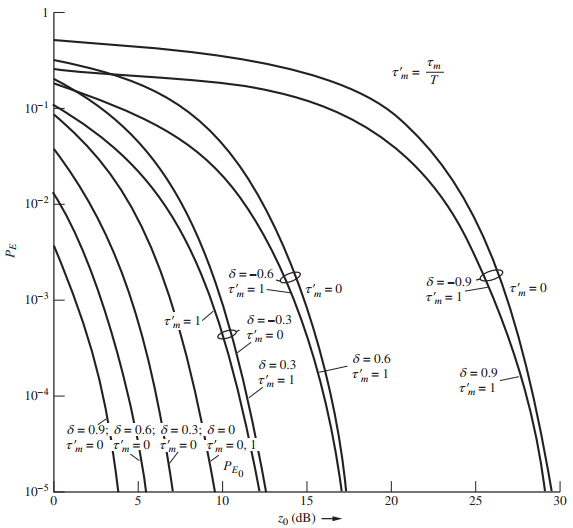
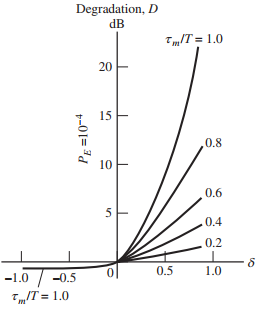
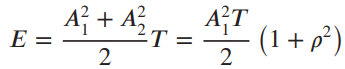
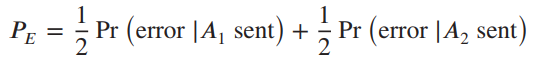
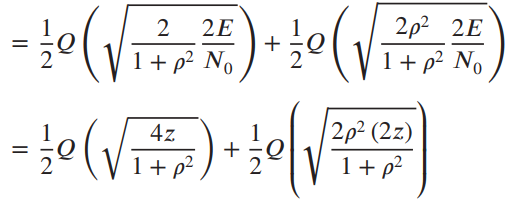
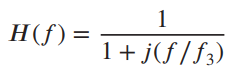
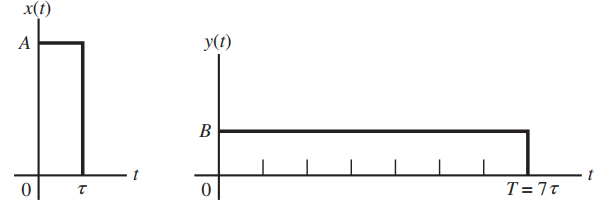
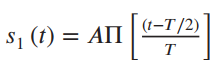
![(1–T/2) $2 (1) = ]}=4 1+ cos 2 2a(1–T/2) т](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1537/8/7/7/0145baa2416c4f3f1537859390674.jpg)
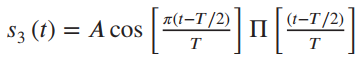
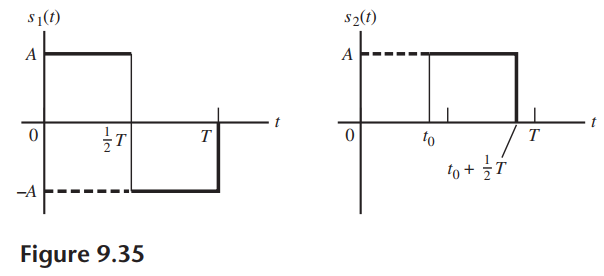
![[(( — т/2) н0] SA(1) 3D АП 꾸의피의 ауe) (t – T /2)] П л (1 — Т/2) Sв (1) 3 Всos т мо-9( (t –](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1537/8/7/7/2925baa252cb47d31537859668563.jpg)
![[(t – T /2)] SĄ(t) = AII 2 (t – 3T /4)] AII 2 (t – T /4) AII SB(t)](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1537/8/7/8/5655baa2a256e3171537860940654.jpg)
![[4 (t – T /8) 4 (t – 3T /8)] АП Sc(t) = AII [4 (t – 5T /8)] 4 (t – 7T /8)] АП +AI](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1537/8/7/8/5785baa2a32843271537860954377.jpg)