![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()




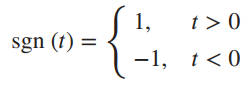
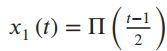
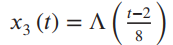
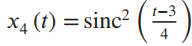
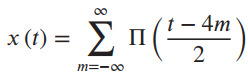
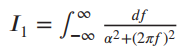
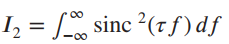
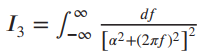
![[1+cos (2@,t)] To 2t y(t) =](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1536/6/6/4/3695b97a331182da1536646711237.jpg)
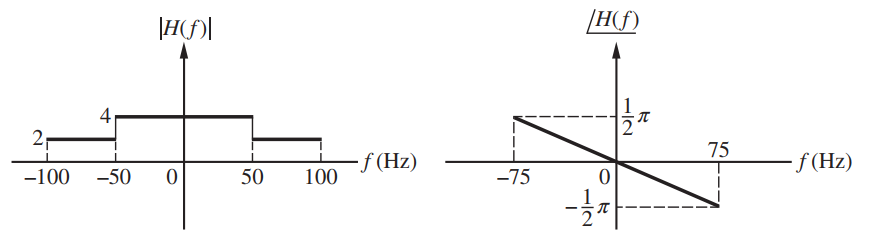
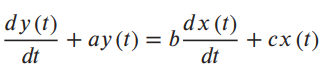
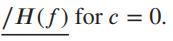
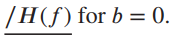
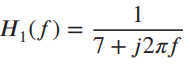
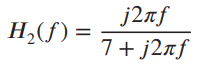
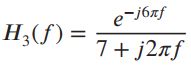
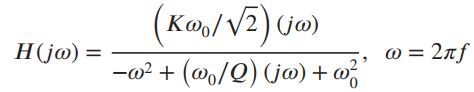
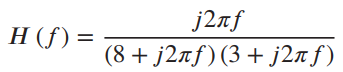
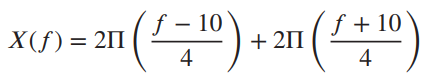
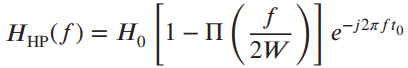
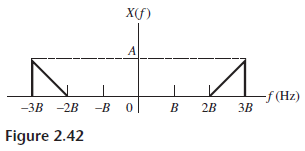
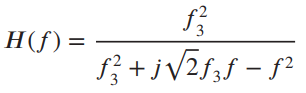
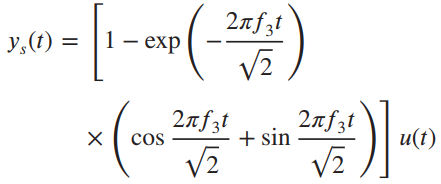
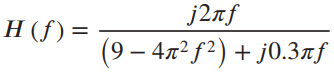
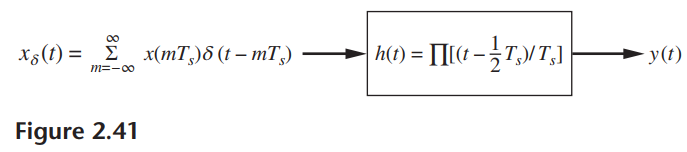
![x(t) X5 (t) h(t) = Y(1) = x,(1) * II(4 - 7)/ 7] Пс-3»я E 8 (t – nT,) 00 n=-00 Figure 2.40](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1536/7/4/8/2415b98ead12606c1536730587811.jpg)