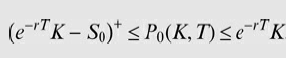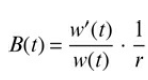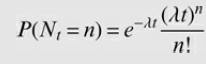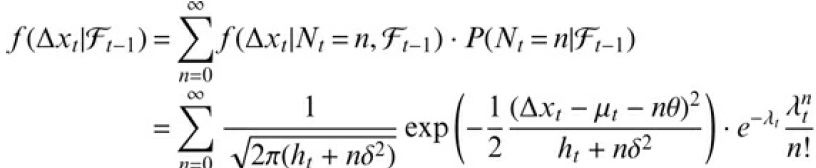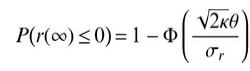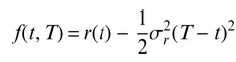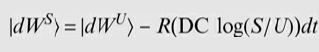![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


![El «]ICm) = W max U[C] subject to |C).CM) m=1](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1542/0/1/4/6745be946d21133a1541997193606.jpg)
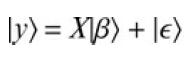
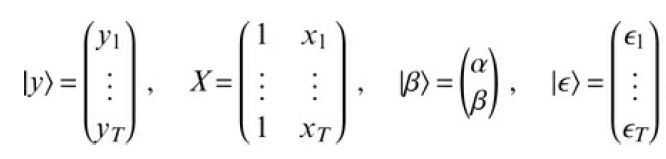
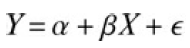
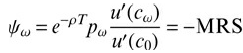
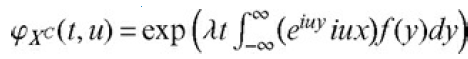
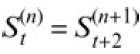
![В, %3 о' ЕТ В+к1F1 = 6 E[ Brk\Fi]](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1542/0/4/2/1475be9b22364f4c1542024667367.jpg)
![r=- log E[M,|Fi-1] =p+ y(g + (1 – ø)(5 - $i-1)) – ro?(1 + A(s81-1))² =p+ yg - (1 – $), =p+ yg - 2](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1542/1/0/0/9895bea97fdaf52f1542028983708.jpg)
![Eļu(X)] = log(2](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1542/1/0/6/0995beaabf303fbf1542088627183.jpg)