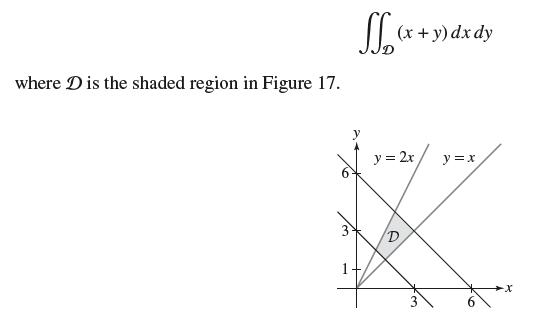
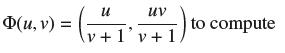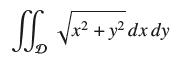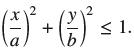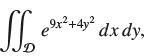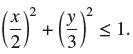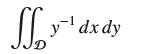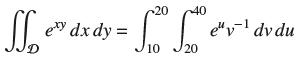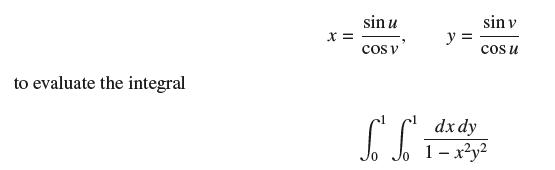![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()



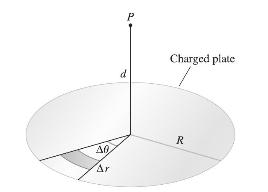
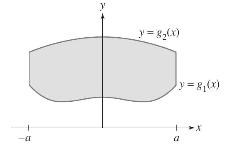
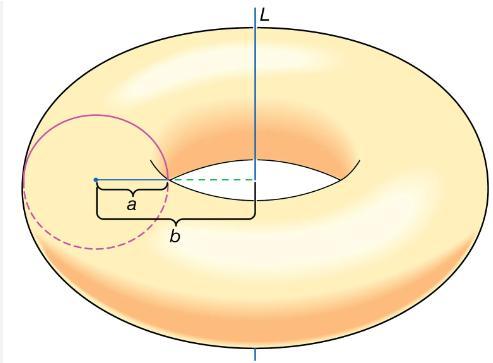
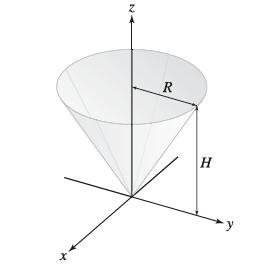
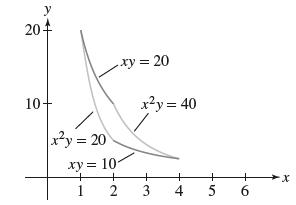
![xy dx dy as an integral over Do = [0, 1] [0, 1]. D](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/6/6/0/56665aa5096233fc1705660565767.jpg)
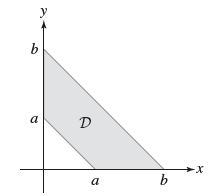
![EXAMPLE 3 Let G(u, v) = (uv, uv) for u> 0, v> 0. Determine the images of (b) [1,2] x [1,2] (a) The lines u =](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/6/6/1/92365aa55e396e2a1705661923233.jpg)