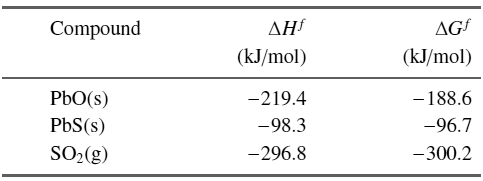
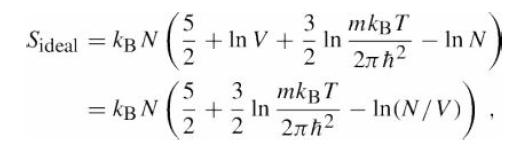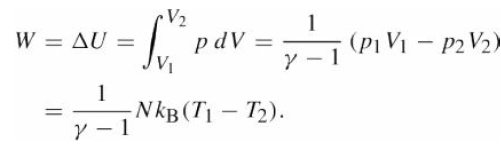![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


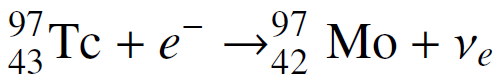
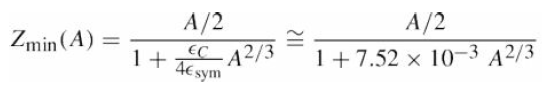
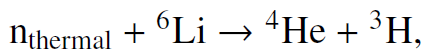
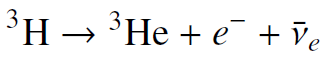
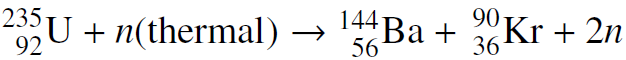
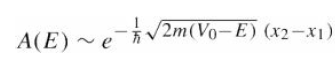
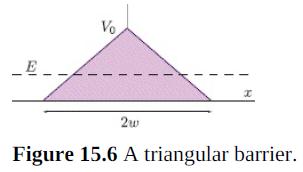
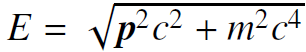
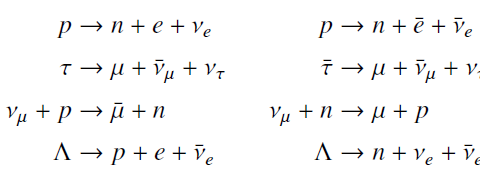
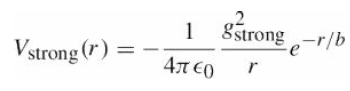
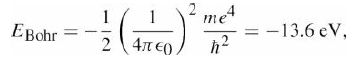
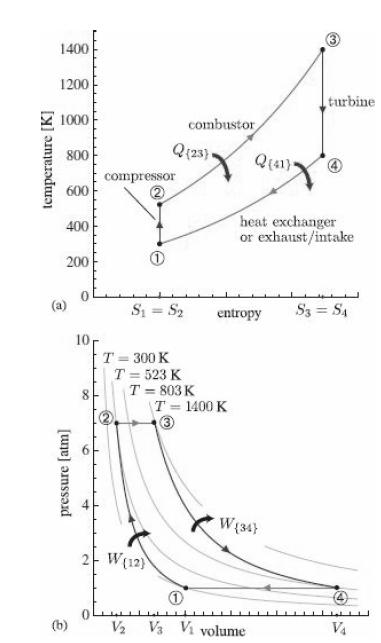
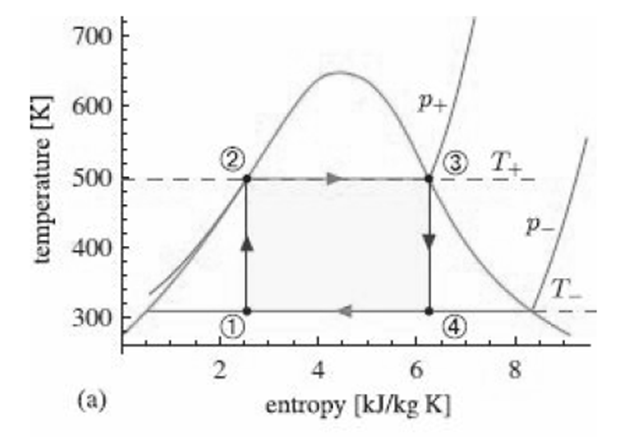
![700 P+ 600 о т. 500 p- 400 т. 300 4 6. (a) entropy [kJ/kg K] 3, т. 800 700 P+ 600 Tvap (P) 500 p- 400 т. 300 4 8. (](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1547/7/3/0/4685c407e24ad0c11547713112571.jpg)
![800 700 p. 600 500 Tregen 6. 400 1-f 300 т. p- 4 (b) entropy [kJ/kg K] temperature [K] 2.](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1547/7/2/6/1475c406d438691c1547708791667.jpg)
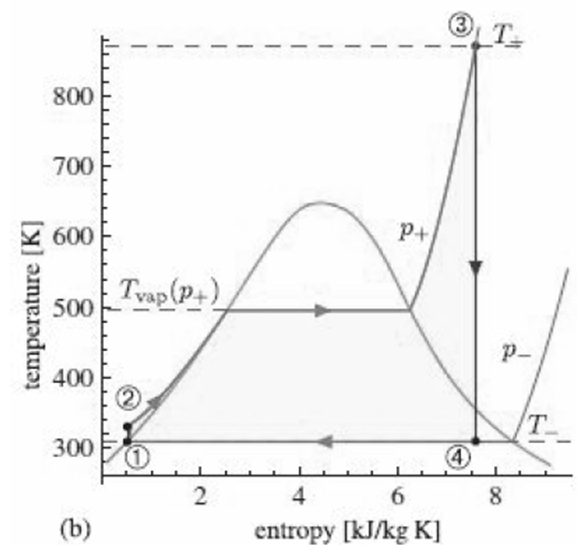
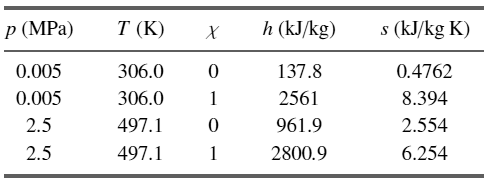
![700 K 40 650 K 20 600 K 10 550 K X. 500 K 0.005 0.01 specific volume [m/kg] 0.001 0.05 0.1 0.5 (a) critical 40 point 20](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1547/7/2/6/3665c406e1ece5c91547709010890.jpg)
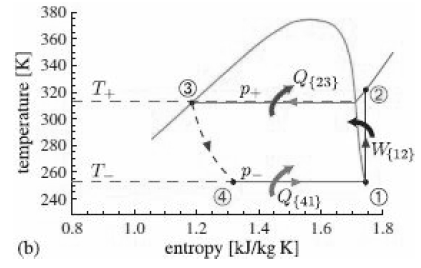
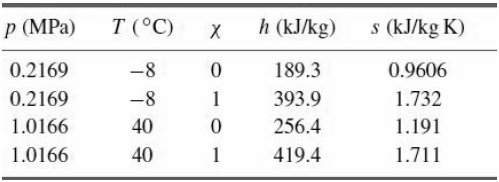
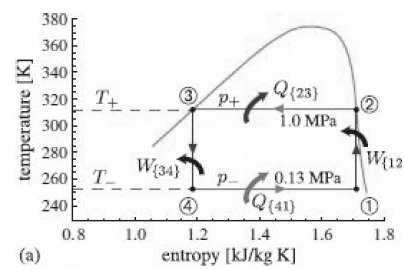
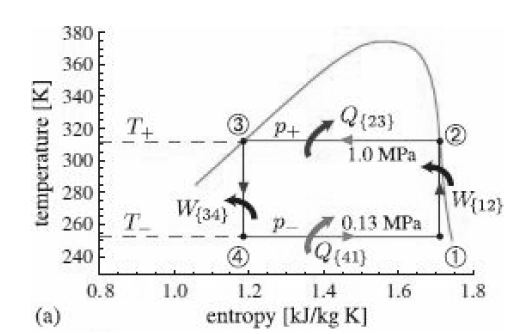
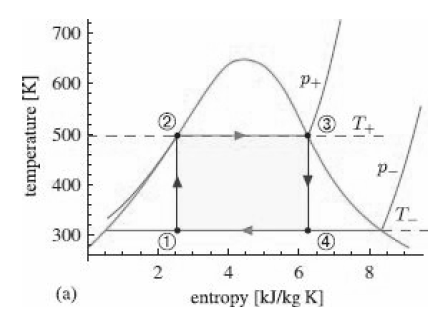
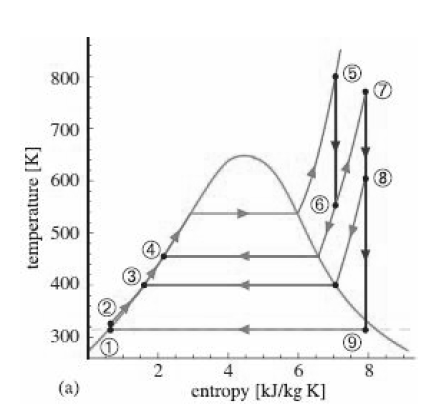
![p(Tsat) 1x 10° Pa (99.61°C) 1.2 x 10° Pa (104.78 °C) h Temp [°C] [m*kg] [m*/kg] [kJ/kg] [kJ/kg] [kJ/kg K] [kJ/kg] [k/kg] [kJ/kg K] Sat. Lig. 1.0432 x 10 3 Evap. Sat. Vap. 3. 439.23 1.0473 x 10 1.4274 439.36 2243.7 2683.1 1.3609 5.9368 417.40 417.40 1.3028 1.6929 6.0560 2088.2](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1607/6/7/0/9095fd31c7d467341607670907728.jpg)
![p(Tsat) 1x 10° Pa (99.61°C) 1.2 x 10° Pa (104.78 °C) h Temp [°C] [m*kg] [m*/kg] [kJ/kg] [kJ/kg] [kJ/kg K] [kJ/kg] [k/kg] [kJ/kg K] Sat. Lig. 1.0432 x 10 3 Evap. Sat. Vap. 3. 439.23 1.0473 x 10 1.4274 439.36 2243.7 2683.1 1.3609 5.9368 417.40 417.40 1.3028 1.6929 6.0560 2088.2](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1607/6/7/0/8765fd31c5c00d561607670874621.jpg)
![p(Tsat) 1x 10° Pa (99.61°C) 1.2 x 10° Pa (104.78 °C) h Temp [°C] [m*kg] [m*/kg] [kJ/kg] [kJ/kg] [kJ/kg K] [kJ/kg] [k/kg] [kJ/kg K] Sat. Lig. 1.0432 x 10 3 Evap. Sat. Vap. 3. 439.23 1.0473 x 10 1.4274 439.36 2243.7 2683.1 1.3609 5.9368 417.40 417.40 1.3028 1.6929 6.0560 2088.2](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1607/6/7/0/7185fd31bbecc95c1607670717130.jpg)