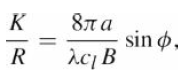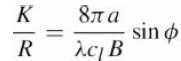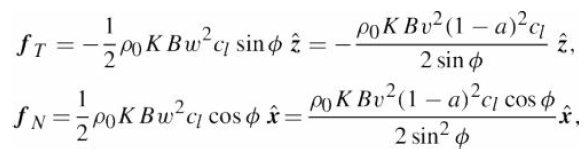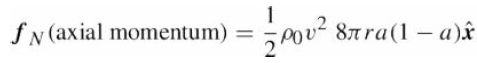![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


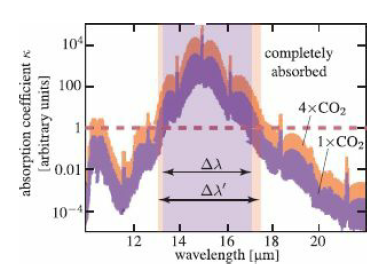
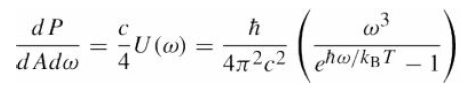
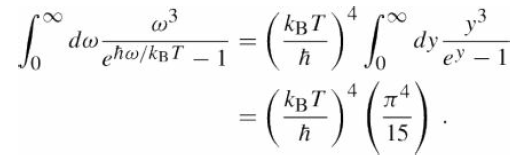
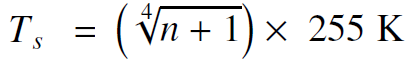
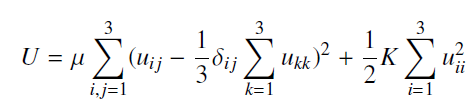
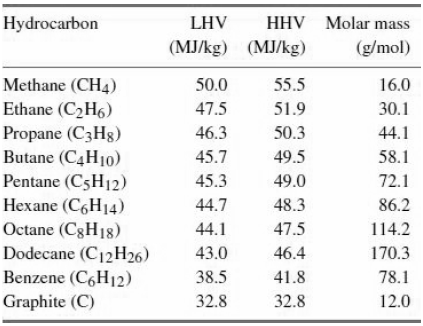
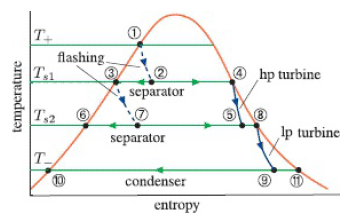
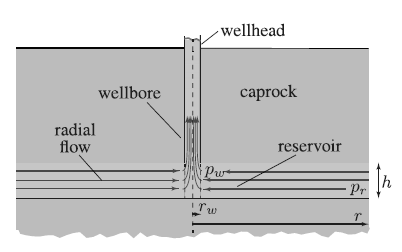
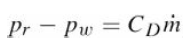
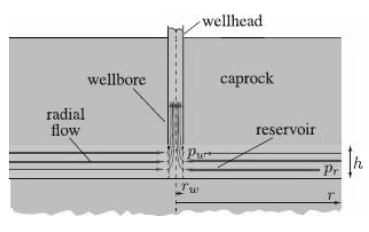
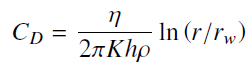
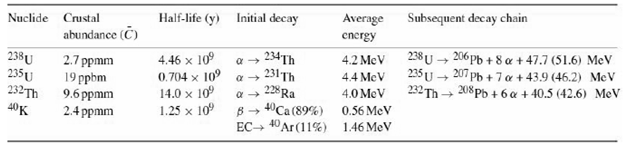
![O = 98CU + 26.5CTH + 0.0035Ck[µW/kg]](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1548/1/8/1/4635c475fd74f4e01548164113802.jpg)