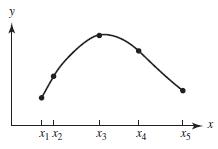
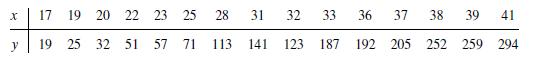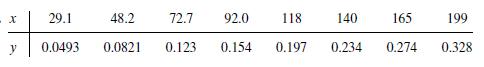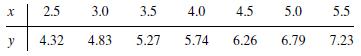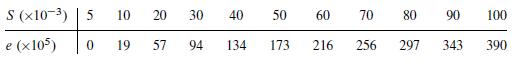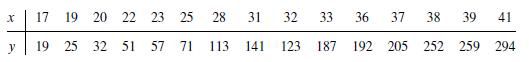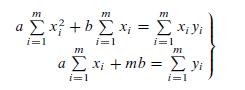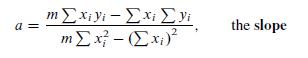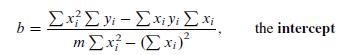![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


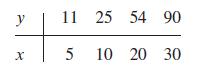
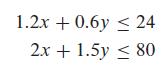
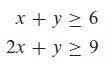
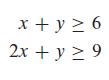
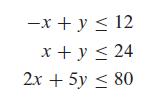
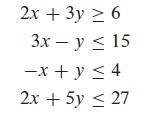
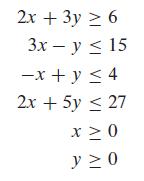

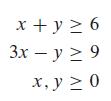
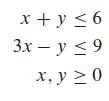
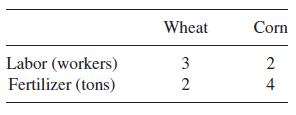
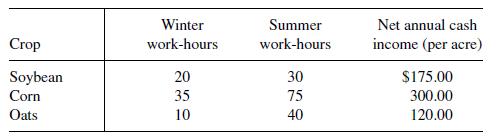
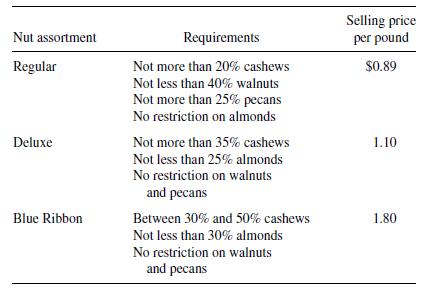
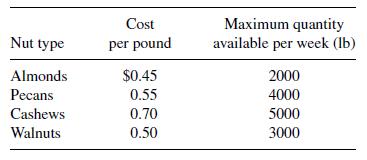
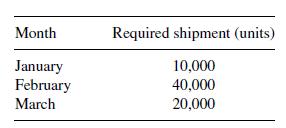
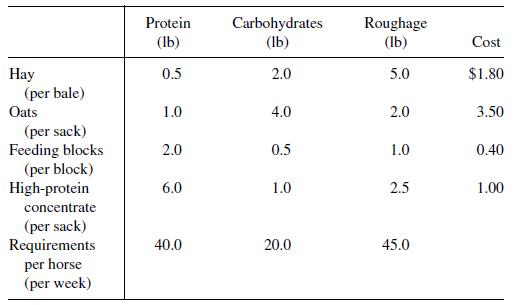
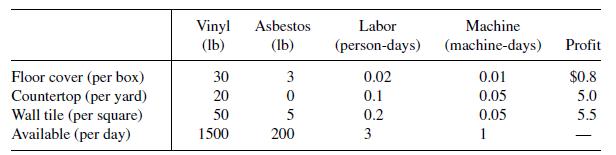
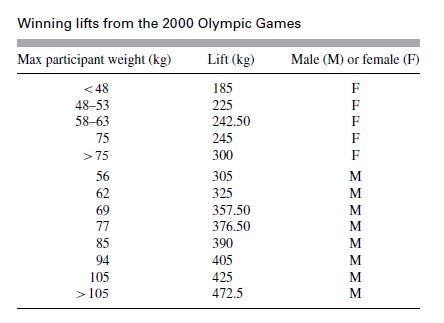
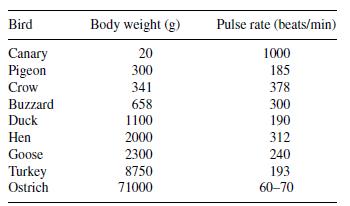
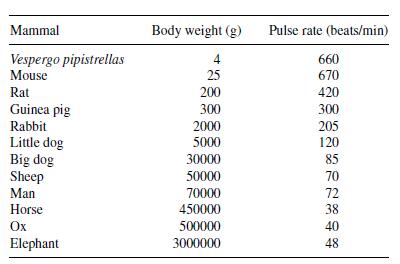
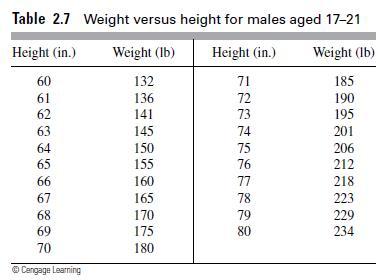
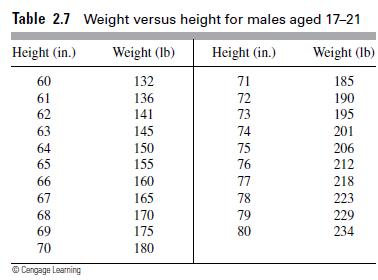
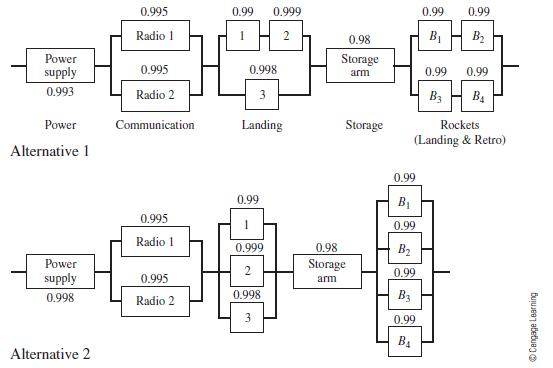
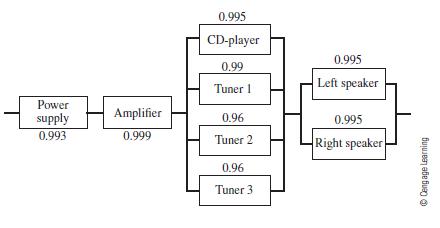
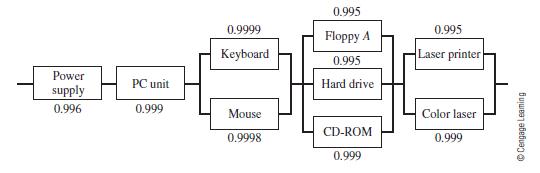
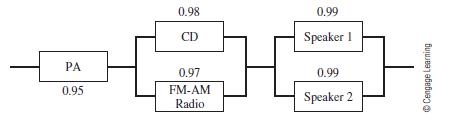
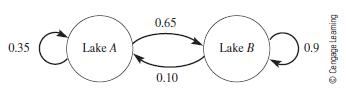
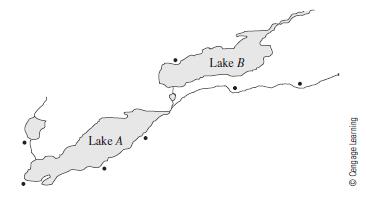
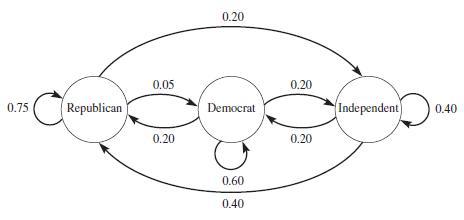
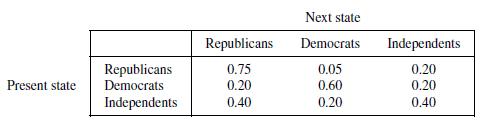
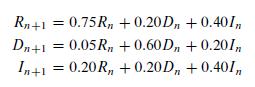
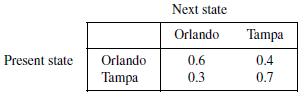
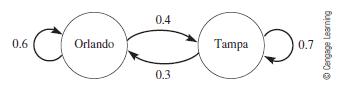
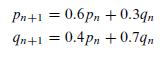
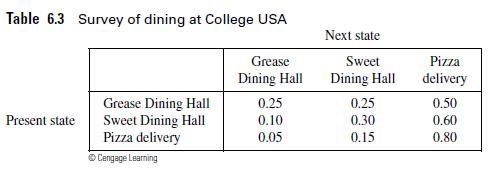
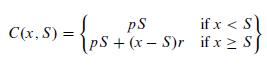
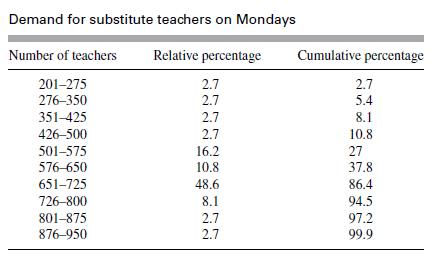

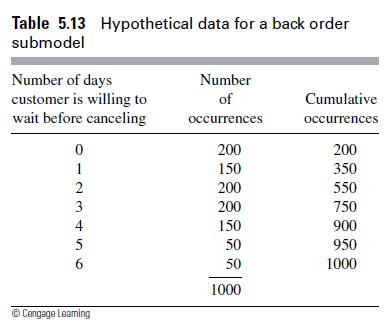
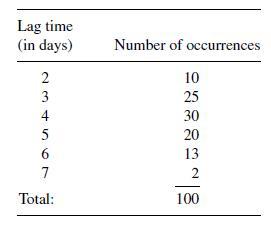
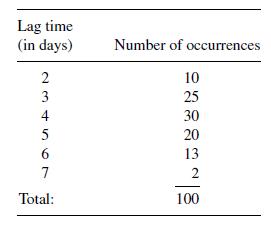
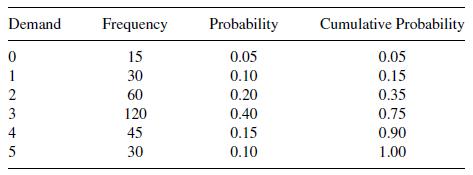
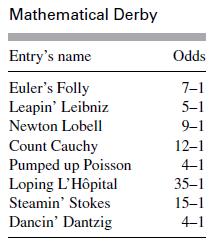
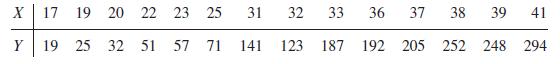

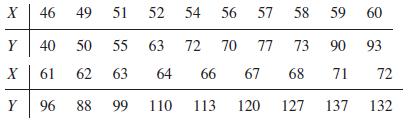
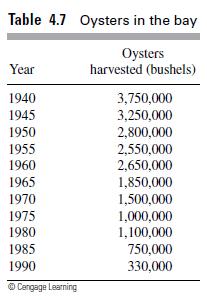
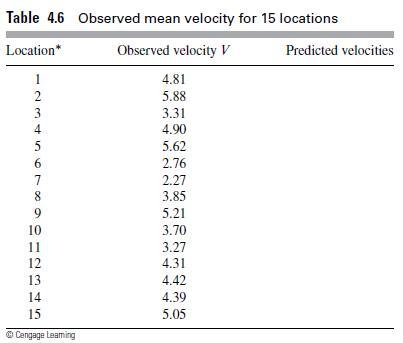
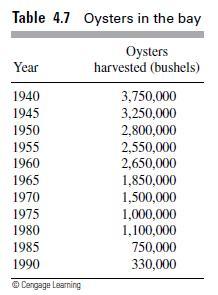
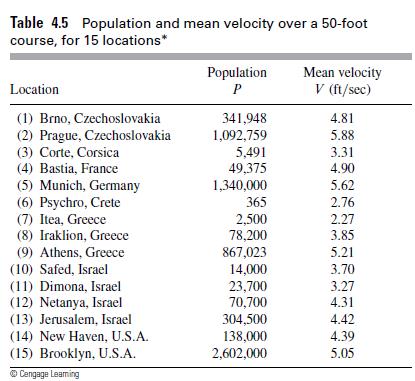
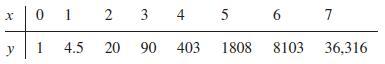
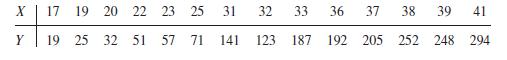
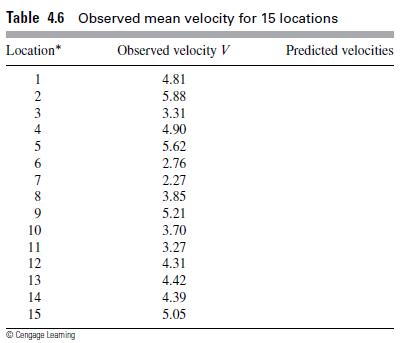
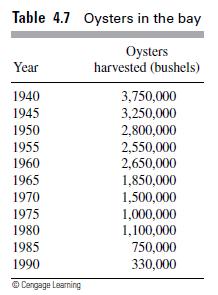
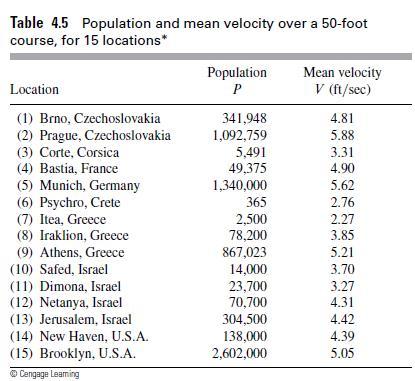
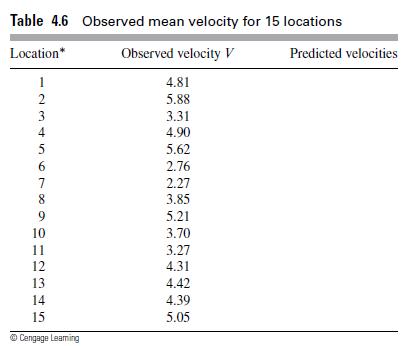
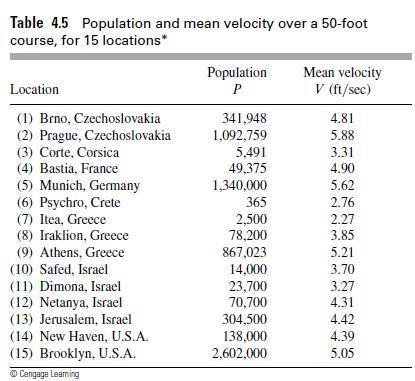
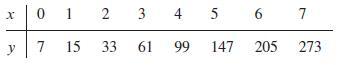
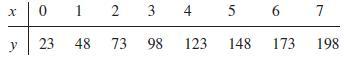
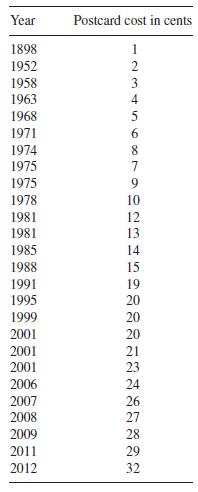
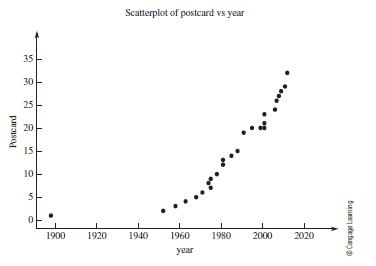
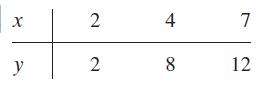
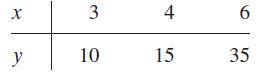
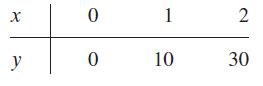



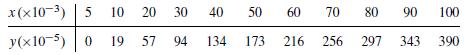

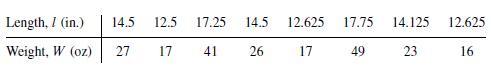

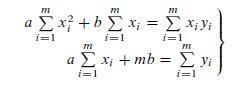
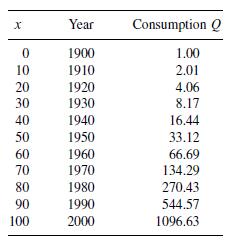
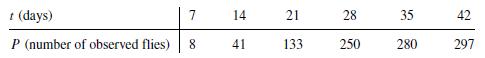
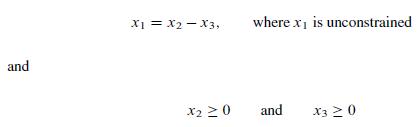
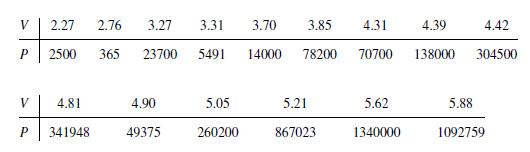

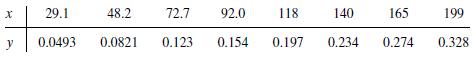
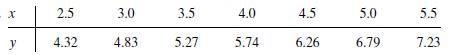
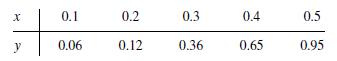
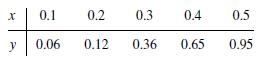
![m x +b 2 x = = i=l i=l 777 xivi i=l 777 a xi + mb = i=l i=]](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1704/1/1/6/6056592c17d2cd311704116604145.jpg)